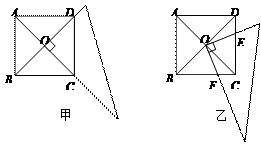
将一块三角板的直角顶点放在正方形ABCD的对角线交点位置,两边与对角线重合如图甲,将这块三角板绕直角顶点顺时针方向旋转(旋转角小于90°)如图乙.⑴试判断△ODE和△OCF是否全等,并证明你的结论.
⑵若正方形ABCD的对角线长为10,试求三角板和正方形重合部分的面积.
(8分) 现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.



图(1)图(2)图(3)图(4)
观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征
(12分)某公司在A、B两地分别有库存机器16台和12台,现要运往甲、乙两地,其中甲地15台,已地13台,从A地运一台到甲地的运费为500元,到乙地的运费为400元,从B地运一台到甲地的运300元,到乙地为600元,公司应怎样设计调运方案,能使这些机器的总运费最省?最省运费是多少?(设从A运到甲地的机器为X台,总运费为Y元)。
(8分)已知:如图,AB=AE,BC=ED,AF⊥CD且F是CD的中点, 求证:∠B=∠E.
求证:∠B=∠E.
(8分)如右图,AC与BD交于O点,有如下三个关系式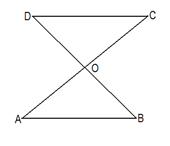
①OA=OC,②OB=OD,③AB∥CD。(1)请用其中两个关系式作为条件,另一个关系式作为结论,写出一个真命题。
已知:_________________,求证:_____(填序号,就可以)
(2)证明(1)中你写出的真命题。
.(8分)先化简,再求值: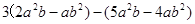 ,其中
,其中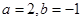 。
。