（年云南省昆明市）如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15cm，CD=20cm，AB和CD之间有一景观池，小南在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°（点B、E、D在同一直线上），求两幢建筑物之间的距离BD（结果精确到0．1m）．（参考数据：sin42°≈0．67，cos42°≈0．74，tan42°≈0．90）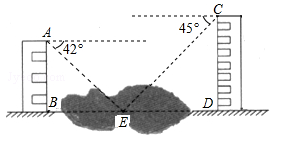
（1）解方程：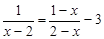
；（2）解不等式组：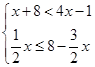
计算或化简：
（1）计算：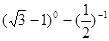
＋|2−3|＋sin245°
（2）先化简，再求值：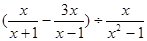
，其中x＝－2.
操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点（不包括射线的端点）.如图1，2，3是旋转三角板得到的图形中的3种情况.
研究：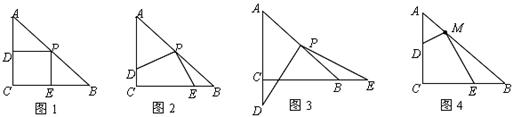
（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合如图2加以证明；
（2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长；若不能，请说明理由；
（3）若将三角板的直角顶点放在斜边AB上的M处，且AM∶MB＝1∶3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合如图4加以证明.
如图，一条直线与反比例函数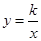
的图象交于A（1，4）B（4，n）两点，与
轴交于D点，AC⊥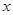轴，垂足为C．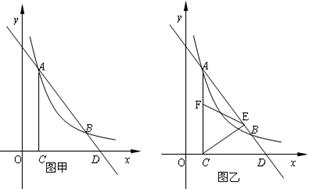
（1）如图甲，①求反比例函数的解析式；②求n的值及D点坐标；
（2）如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．试说明△CDE∽△EAF；
为了测量路灯（OS）的高度，把一根长1.5米的竹竿（AB）竖直立在水平地面上,测得竹竿的影子（BC）长为1米，然后拿竹竿向远离路灯方向走了3.2米（BB‘），再把竹竿竖立在地面上，测得竹竿的影长（B‘C‘）为1.8米，求路灯离地面的高度.