(年云南省)为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: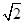 ≈1.41,
≈1.41,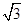 ≈1.73,结果保留整数)
≈1.73,结果保留整数)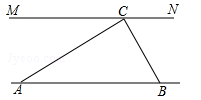
某学校班主任暑假带领该班三好学生去旅游,甲旅行社说:“如果教师买全票一张,其余学生享受半价优惠” ;乙旅行社说:“教师在内全部按票价的6折优惠” ;若全票价格是240元/张.
(1)如果有10名学生,应选择哪个旅行社,并说出理由;
(2)当学生人数是多少时,两家旅行社收费一样多.
如图,有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的图形,小明将这四张牌背面朝上洗匀后随机摸出一张,放回后洗匀再随机摸出一张。
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用A、B、C、D表示)
(2)求两次摸牌的牌面图形既是中心对称图形又是轴对称图形的概率。
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为A(-2,3)B(-3,1)
(1)画出△AOB绕点O顺时针旋转 后的△
后的△ ;
;
(2)写出点 的坐标;
的坐标;
(3)求四边形 的面积.
的面积.
如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1.0),C(0,﹣3).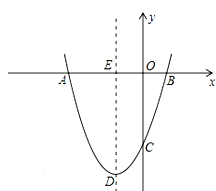
(1)求抛物线的解析式;
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
利达经销店为某工厂代销一种建筑材料.当每千克售价为260元时,月销售量为45千克.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每千克售价下降10元时,月销售量就会增加5千克.综合考虑各种因素,每售出一千克建筑材料共需支付厂家及其它费用100元.设每千克材料售价为x(元),该经销店的月利润为y(元).
(1)当每千克售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每千克多少元?