已知点A(1,a)在抛物线y=x2上.
(1)求A点的坐标;
(2)在x轴上是否存在点P,使得△OAP是等腰三角形?若存在,求出点P的坐标;若不存在,说明理由.
解下列方程(本题有2小题,每小题4分,满分8分)
(1) 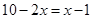 (2)
(2) 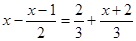
化简(本题有2小题,每小题4分,满分8分)
(1)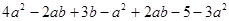 (2)
(2) 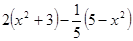
(本题3分+3分+4分)如图,已知二次函数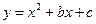 的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(
的图象与x轴交于A、B两点,与y轴交于点P,顶点为C(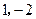 )。
)。
(1)求此函数的关系式;
(2)作点C关于x轴的对称点D,顺次连接A、C、B、D.若在抛物线上存在点E,使直线PE将四边形ACBD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标;若不存在,请说明理由。
(本题3分+3分+4分)施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).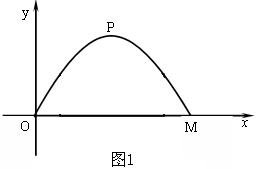
⑴求出这条抛物线的函数解析式,并写出自变量x的取值范围;
⑵隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
⑶施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上。B、C点在地面OM线上(如图2所示).为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.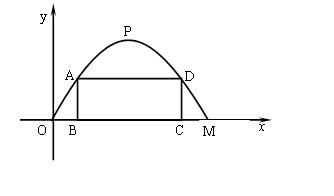
|
(本题2分+3分+4分)某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件,后来经过市场调查,发现这种商品每降低1元,其销量可增加10件。
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价x元,商场一天可获利y元。
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出y与x之间的函数关系式,并通过画该函数图像的草图,观察其图象的变化趋势,结合题意写出该x取何值时,商场所获利润不少于2160元?