.(本小题满分12分)已知椭圆的中心在原点,焦点在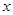 轴上,一个顶点为
轴上,一个顶点为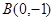 ,且其右焦点到直线
,且其右焦点到直线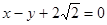 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)是否存在斜率为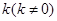 ,且过定点
,且过定点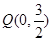 的直线
的直线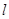 ,使
,使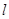 与椭圆交于两个不同的点
与椭圆交于两个不同的点 、
、 ,且
,且 ?若存在,求出直线
?若存在,求出直线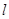 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)
已知函数
(I)若 的极值;
的极值;
(II)设 成立,求实数a的取值范围。
成立,求实数a的取值范围。
(本小题满分12分) 已知抛物线
已知抛物线
(I)求p与m的值;
(II)设抛物线G上一点P的横坐标t,过点P引斜率 为—1的直线l交抛物线G于另一点A,交x轴于点B,若|OA|=|OB|(O为坐标原点),求点P的坐标。
为—1的直线l交抛物线G于另一点A,交x轴于点B,若|OA|=|OB|(O为坐标原点),求点P的坐标。
(本小题满分10分)
小正方形按照如图规律排列,用 表示图(n)中小正方形的个数(n为正整数)。
表示图(n)中小正方形的个数(n为正整数)。
(I)按照如图规律写出 的值;
的值;
(II)合情推理写出 的表达式,并简要写出推理过程。
的表达式,并简要写出推理过程。
(本小题满分12分)
已知椭圆的两焦点为
(I)求此椭圆的方程;
(II)设直线 与此椭圆相交于不同的两点,求m的取值范围.
与此椭圆相交于不同的两点,求m的取值范围.
(本小题满分12分)
在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是看电视,另外30人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外30人主要的休闲方式是运动。 (I)根据以上数据建立一个2×2的列联表:
(I)根据以上数据建立一个2×2的列联表:
| 休闲方式 性别 |
 看电视 看电视 |
运动 |
总计 |
| 女性 |
|||
| 男性 |
|||
| 总计 |
(II)休闲方式与性别是否有关?