(本题12分)设函数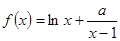 在
在 内有极值。
内有极值。
(1)求实数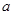 的取值范围;
的取值范围;
(2)若 分别为
分别为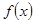 的极大值和极小值,记
的极大值和极小值,记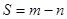 ,求S的取值范围。
,求S的取值范围。
(注: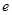 为自然对数的底数)
为自然对数的底数)
(本小题满分10分)如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA 平面ABCD,
平面ABCD,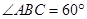 ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(1)证明:AE⊥PD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正 切值为 ,求二面角E—AF—D的余弦值.
,求二面角E—AF—D的余弦值.
(本小题满分10分)某研究性学习小组对某花卉种子的发芽率与昼夜温差之间的关系进行研究.他们分别记录了3月1日至3月5日的昼夜温差及每天30颗种子的发芽数,并得到如下资料:
| 日期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
| 温差x (度) |
10 |
11 |
13 |
12 |
9 |
| 发芽数y(颗) |
15 |
16 |
17 |
14 |
13 |
参考数据 ,其中
,其中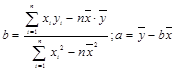
(1)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程.据气象预报3月6日的昼夜温差为11℃,请预测3月6日浸泡的30颗种子的发芽数.(结果保留整数)
(2)从3月1日至3月5日中任选两天,记种子发芽数超过15颗的天数为X,求X的概率分布列,并求其数学期望和方差.
(本小题满分10分)已知单调递增的等比数列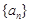 满足:
满足: ,且
,且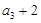 是
是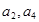 的等差中项.
的等差中项.
(1)求数列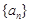 的通项公式;
的通项公式;
(2)若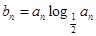 ,
,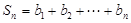 ,求使
,求使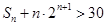 成立的正整数
成立的正整数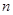 的最小值.
的最小值.
(本小题满分16分)已知数列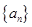 的奇数项是首项为
的奇数项是首项为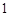 的等差数列,偶数项是首项为
的等差数列,偶数项是首项为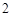 的等比数列,数列
的等比数列,数列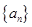 前
前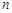 项和为
项和为 ,且满足
,且满足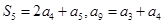 .
.
(1)求数列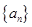 的通项公式;
的通项公式;
(2)若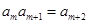 ,求正整数
,求正整数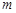 的值;
的值;
(3)是否存在正整数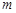 ,使得
,使得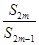 恰好为数列
恰好为数列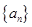 中的一项?若存在,求出所有满足条件的
中的一项?若存在,求出所有满足条件的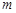 值,若不存在,说明理由.
值,若不存在,说明理由.
(本小题满分16分)设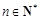 ,函数
,函数
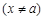 ,其中常数a
,其中常数a .
.
(1)求函数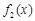 的极值;
的极值;
(2)设一直线与函数 的图象切于两点A(x1,y1),B(x2,y2),且
的图象切于两点A(x1,y1),B(x2,y2),且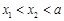 .
.
①求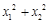 的值;
的值;
②求证: .
.