【2015高考四川,文16】设数列{an}(n=1,2,3…)的前n项和Sn满足Sn=2an-a3,且a1,a2+1,a3成等差数列.
(Ⅰ)求数列的通项公式;
(Ⅱ)设数列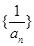 的前n项和为Tn,求Tn.
的前n项和为Tn,求Tn.
【2015高考陕西,文21】设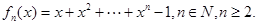
(Ⅰ)求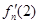 ;
;
(Ⅱ)证明: 在
在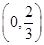 内有且仅有一个零点(记为
内有且仅有一个零点(记为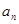 ),且
),且 .
.
【2015高考山东,文19】已知数列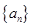 是首项为正数的等差数列,数列
是首项为正数的等差数列,数列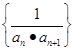 的前
的前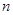 项和为
项和为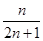 .
.
(Ⅰ)求数列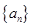 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列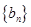 的前
的前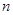 项和
项和 .
.
【2015高考湖南,文21】 (本小题满分13分)函数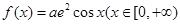 ,记
,记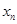 为
为 的从小到大的第
的从小到大的第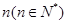 个极值点。
个极值点。
(Ⅰ)证明:数列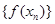 是等比数列;
是等比数列;
(Ⅱ)若对一切 恒成立,求
恒成立,求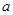 的取值范围。
的取值范围。
【2015高考湖南,文19】(本小题满分13分)设数列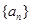 的前
的前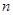 项和为
项和为 ,已知
,已知 ,且
,且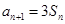
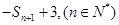 ,
,
(Ⅰ)证明: ;
;
(Ⅱ)求 。
。