提高南洋大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度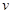
（单位：千米/小时）是车流密度
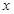（单位：辆/千米）的函数．当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当
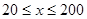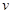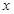时，车流速度是车流密度的一次函数．
（Ⅰ）当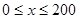
时，求函数
的表达式； （Ⅱ）当车流密度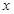为多大时，车流量（单位时间内通过桥上某观测点的车辆数，单位：辆/小时） 
可以达到最大，并求出最大值．（精确到1辆/小时）
（本小题满分12分）
设函数f（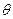
）=
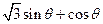，其中，角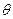的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P（x,y），且
.
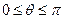（1）若点P的坐标为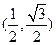
，求
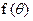的值；
（II）若点P（x，y）为平面区域Ω：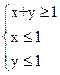
，上的一个动点，试确定角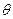的取值范围，并求函数
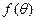的最小值和最大值.
（本小题满分12分）
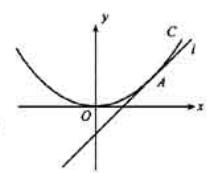
如图，直线l ：y=x+b与抛物线C ：x2=4y相切于点A。
（1）求实数b的值；
（11）求以点A为圆心，且与抛物线C的准线相切的圆的方程.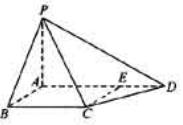
（本小题满分14分）
已知a，b为常数，且a≠0，函数
（e=2.71828…是自然对数的底数）.
（I）求实数b的值；
（II）求函数f（x）的单调区间；
（III）当a=1时，是否同时存在实数m和M（m<M），使得对每一个t∈[m，M]，直线y=t与曲线
都有公共点？若存在，求出最小的实数m和最大的实数M；若不存在，说明理由.
（本小题满分12分）
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。
（1）求证：CE⊥平面PAD；
（11）若PA=AB=1，AD=3，CD=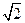
，∠CDA=45°，求四棱锥P-ABCD的体积
（本小题满分12分）
某日用品按行业质量标准分成五个等级，等级系数X依次为1，2，3，4，5.现从一批该日用品中随机抽取20件，对其等级系数进行统计分析，得到频率分布表如下：
（1）若所抽取的20件日用品中，等级系数为4的恰有3件，等级系数为5的恰有2件，求a、b、c的值；
（11）在（1）的条件下，将等级系数为4的3件日用品记为x1, x2, x3，等级系数为5的2件日用品记为y1,y2，现从x1, x2, x3, y1, y2,这5件日用品中任取两件（假定每件日用品被取出的可能性相同），写出所有可能的结果，并求这两件日用品的等级系数恰好相等的概率.