（本小题满分12分）
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB。
（1） 求证：CE⊥平面PAD；
（11）若PA=AB=1，AD=3，CD=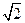
，∠CDA=45°，求四棱锥P-ABCD的体积
已知函数f(x)=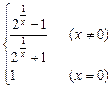
(1)f(x)在x=0处是否连续？说明理由；
(2)讨论f(x)在闭区间［－1,0］和［0,1］上的连续性.
已知函数f(x)=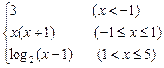
(1)讨论f(x)在点x=－1,0,1处的连续性；
(2)求f(x)的连续区间。
求证:方程x=asinx+b(a＞0,b＞0)至少有一个正根，且它不大于a+b.
已知函数f(x)=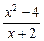
,
(1)求f(x)的定义域，并作出函数的图像；
(2)求f(x)的不连续点x0;
(3)对f(x)补充定义，使其是R上的连续函数.
袋子A和B中装有若干个均匀的红球和白球，从A中摸出一个红球的概率是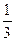
，从B中摸出一个红球的概率为p．
(Ⅰ) 从A中有放回地摸球，每次摸出一个，有3次摸到红球即停止．
(i)求恰好摸5次停止的概率；
(ii)记5次之内(含5次)摸到红球的次数为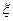
，求随机变量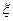的分布率及数学期望E．
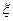(Ⅱ) 若A、B两个袋子中的球数之比为12，将A、B中的球装在一起后，从中摸出一个红球的概率是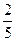
，求p的值．