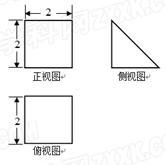
(本小题满分14分)三棱柱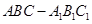 的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,
的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,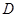 为
为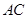 的中点.
的中点.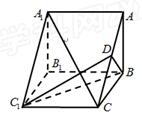
(1)求证: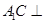 平面
平面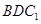 ;
;
(2)求二面角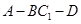 的正切值.
的正切值.
如图所示,在矩形ABCD中,AB=4,AD=2 ,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
,E是CD的中点,O为AE的中点,以AE为折痕,将△ADE向上折起,使D到P,且PC=PB
(1)求证:PO⊥面ABCE;
(2)求AC与面PAB所成角 的正弦值.
的正弦值.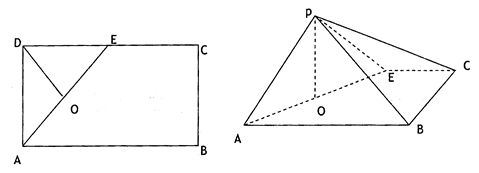
(本小题满分12分)
某菜园要将一批蔬菜用汽车从所在城市甲运至亚运村乙,已知从城市甲到亚运村乙只有两条公路,且运费由菜园承担. 若菜园恰能在约定日期(
若菜园恰能在约定日期(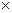 月
月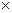 日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提
日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提 前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.为保证蔬菜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送蔬菜,已知下表内的信息:
前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.为保证蔬菜新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送蔬菜,已知下表内的信息: (注:毛利润
(注:毛利润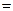 销售商支付给菜园的费用
销售商支付给菜园的费用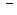 运费)
运费)
(Ⅰ) 记汽车走公路1时菜园获得的毛利润为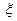 (单位:万元),求
(单位:万元),求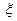 的分布列和数学期望
的分布列和数学期望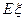 ;
;
(Ⅱ) 假设你是菜园的决策者,你选择哪条公路运送蔬菜有可能让菜园获得的毛利润更多?
(本小题满分12分)
已知函数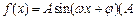 >0,
>0,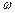 >0,
>0,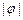 <
<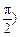 的图象与
的图象与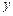
轴的交点为(0,1),它在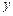 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为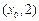 和
和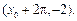
(1)写出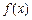 的解析式及
的解析式及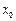 的值
的值 ;
;
(2)若锐角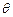 满足
满足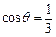 ,求
,求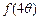 的值.
的值. 
(本小题满分14分)
抛物线D以双曲线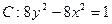 的焦点
的焦点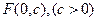 为焦点
为焦点 .
.
(1)求抛物线D的 标准方程;
标准方程;
(2)过直线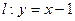 上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐
上的动点P作抛物线D的两条切线,切点为A,B.求证:直线AB过定点Q,并求出Q的坐 标;
标;
(3)在(2)的条件下,若直线PQ交抛物线D于M,N两点,求证:|PM|·|QN|=|QM|·|PN|
(本小题满分13分)
已知数列{an}中,a2=p(p是不等于0的常数),Sn为数列{an}的前n项和,若对任意的正整数n 都有Sn=.
都有Sn=.
(1)证明:数列{an}为等差数列;(2)记 bn=+,求数列{bn}的前n项和Tn;
bn=+,求数列{bn}的前n项和Tn;
(3)记cn=Tn-2n,是否存在正整数N,使得当n>N时,恒有cn∈(,3),若存在,请证明你的结论,并给出一个具体的N值;若不存在,请说明理由.