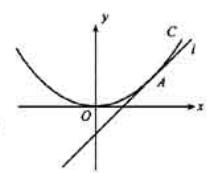
（本小题满分12分）如图，直线l：yxb与抛物线C：x24y-优题课

题文

（本小题满分12分）
如图，直线l ：y=x+b与抛物线C ：x²=4y相切于点A。
（1）求实数b的值；
（11）求以点A为圆心，且与抛物线C的准线相切的圆的方程.

科目数学题型解答题难度中等

相关试题

某种产品的质量以其质量指标值衡量，质量指标值越大表明质量越好，且质量指标值大于或等于102的产品为优质品，现用两种新配方（分别称为 $A$ 配方和 $B$ 配方）做试验，各生产了100件这种产品，并测量了每件产品的质量指标值，得到下面试验结果：

$A$ 配方的频数分布表

$B$ 配方的频数分布表

（1）分别估计用 $A$ 配方， $B$ 配方生产的产品的优质品率；
（2）已知用B配方生成的一件产品的利润 $y$ (单位：元)与其质量指标值 $t$ 的关系式为 $y = {\begin{matrix} - 2, t < 94 \\ 2, 94 \leq t < 102 \\ t \geq 102 \end{matrix}$ ,
从用 $B$ 配方生产的产品中任取一件，其利润记为 $X$ （单位：元），求X的分布列及数学期望.（以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率）

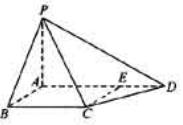
如图，四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为平行四边形， $∠ D A B = 60 °$ , $A B = 2 A D$ , $P D ⊥ 底面 A B C D$ .

（1）证明： $P A ⊥ B D$ ；
（2）若 $P D = A D$ ，求二面角 $A - P B - C$ 的余弦值。

等比数列 ${a_{n_{}}}$ 的各项均为正数，且 $2 a_{1} + 3 a_{2} = 1, {a_{3}}^{2} = 9 a_{2} a_{6}$

（1）求数列 ${a_{n_{}}}$ 的通项公式；
（2）设 $b_{n} = \log_{3} a_{1} + \log_{3} a_{2} + . . . + \log_{3} a_{n}$ 求数列 ${\frac{1}{b_{n}}}$ 的前 $n$ 项和.

设函数 $f (x)$ 定义在 $(0, + \infty)$ 上， $f (1) = 0$ ，导函数 $f ` (x) = \frac{1}{x}$ ， $g (x) = f (x) + f ` (x)$ ．
（1）求 $g (x)$ 的单调区间和最小值；
（2）讨论 $g (x)$ 与 $g (\frac{1}{x})$ 的大小关系；
（3）是否存在 $x_{0} > 0$ ，使得 $|g (x) - g (x_{0})| < \frac{1}{x}$ 对任意 $x > 0$ 成立？若存在，求出 $x_{0}$ 的取值范围；若不存在，请说明理由．

如图， $A$ 地到火车站共有两条路径 $L_{1}$ 和 $L_{2}$ ，据统计，通过两条路径所用的时间互不影响，所用时间落在个时间段内的频率如下表：

时间（分钟）	1020	2030	3040	4050	5060
$L_{1}$ 的频率	$0.1$	$0.2$	$0.3$	$0.2$	$0.2$
$L_{2}$ 的频率	0	$0.1$	$0.4$	$0.4$	$0.1$

现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站．
（1）为了尽最大可能在各自允许的时间内赶到火车站，甲和乙应如何选择各自的路径？
（2）用X表示甲、乙两人中在允许的时间内能赶到火车站的人数，针对（1）的选择方案，求X的分布列和数学期望 .

试卷网试题网古诗词网作文网范文网