如图,地到火车站共有两条路径和,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:

| 时间(分钟) |
10 20 20 |
20 30 30 |
30 40 40 |
40 50 50 |
50 60 60 |
| 的频率 |
|||||
| 的频率 |
0 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站.
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(1)的选择方案,求X的分布列和数学期望 .
抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示 ;
;
| 纪念币 |
A |
B |
C |
| 概率 |
 |
a |
a |
将这三枚纪念币同时抛掷一次,设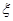 表示出现正面向上的纪念币的个数.
表示出现正面向上的纪念币的个数.
(1)求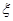 的分布列及数学期望;
的分布列及数学期望;
(2)在概率 中,若
中,若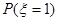 的值最大,求a的最大值
的值最大,求a的最大值
已知曲线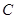 :
: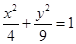 ,直线
,直线 :
: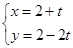 (
( 为参数).
为参数).
(1)写出曲线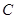 的参数方程,直线
的参数方程,直线 的普通方程;
的普通方程;
(2)过曲线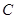 上任一点
上任一点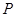 作与
作与 夹角为
夹角为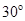 的直线,交
的直线,交 于点
于点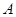 ,求
,求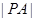 的最大值与最小值.
的最大值与最小值.
两条曲线的极坐标方程分别为 ,它们相交于A,B两点,求线段AB的长.
,它们相交于A,B两点,求线段AB的长.
设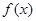 使定义在区间
使定义在区间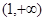 上的函数,其导函数为
上的函数,其导函数为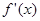 .如果存在实数
.如果存在实数 和函数
和函数 ,其中
,其中 对任意的
对任意的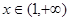 都有
都有 >0,使得
>0,使得 ,则称函数
,则称函数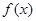 具有性质
具有性质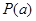 .
.
(1)设函数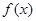
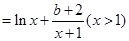 ,其中
,其中 为实数
为实数
①求证:函数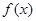 具有性质
具有性质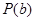 ,②求函数
,②求函数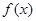 的单调区间.
的单调区间.
(2)已知函数 具有性质
具有性质 ,给定
,给定
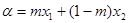 ,
, ,且
,且 ,若|
,若| |<|
|<| |,求
|,求 的取值范围.
的取值范围.
设函数 ,曲线
,曲线 在点(1,
在点(1,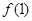 处的切线为
处的切线为 . (Ⅰ)求
. (Ⅰ)求 ;
;
(Ⅱ)证明: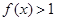 .
.