如图,直线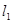 :
: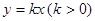 与直线
与直线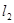 :
: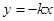 之间的阴影区域(不含边界)记为
之间的阴影区域(不含边界)记为 ,其左半部分记为
,其左半部分记为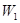 ,右半部分记为
,右半部分记为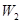 .
.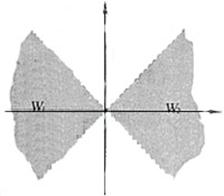
(1)分别用不等式组表示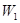 和
和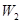 ;
;
(2)若区域 中的动点
中的动点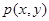 到
到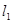 ,
,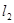 的距离之积等于
的距离之积等于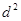 ,求点
,求点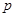 的轨迹
的轨迹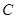 的方程;
的方程;
(本小题满分14分)已知函数 .
.
(1)若a>0,试判断 在定义域内的单调性;
在定义域内的单调性;
(2)若 在
在 上的最小值为
上的最小值为 ,求a的值;
,求a的值;
(3)若 在
在 上恒成立,求a的取值范围
上恒成立,求a的取值范围
(本小题满分13分)已知函数 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为1,求实数a的值;
处的切线斜率为1,求实数a的值;
(2)若函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
(本小题满分12分)在△ABC中,A、B、C为三个内角,f(B)=4cos B·sin2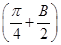 +
+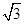 cos 2B-2cos B.
cos 2B-2cos B.
(1)若f(B)=2,求角B;
(2)若f(B)-m>2恒成立,求实数m的取值范围.
(本小题满分12分)设函数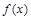 是定义在
是定义在 上的减函数,满足:
上的减函数,满足: ,且
,且 ,求实数m的取值范围.
,求实数m的取值范围.
(本小题满分12分)在△ABC中,角A,B,C所对应的边分别为a,b,c,且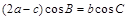 .
.
(1)求角B的大小;
(2)若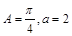 ,求△ABC的面积.
,求△ABC的面积.