如图是一个“有理数转换器”（箭头是指数进入转换器的路径，方框是对进入的数进行转换的转换器）
（1）当小明输入3；—4，
；—201这四个数时，这四次输出的结果分别是：
（2）你认为当输入什么数时，其输出结果是0 ？
（3）你认为这个“有理数转换器”不可能输出什么数？
（4）有一次，小明在操作的时候，输出的结果是2，你判断一下，小明可能输入的是什么数？
如图，直线y =" 2x" + 3与x轴相交于点A，与y轴相交于点B.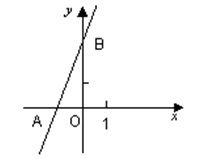
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴的正半轴相交于P，且使OP = 2OA，求ΔABP的面积.
已知点P（2a-12，1-a）位于第三象限.
（1）若点P的纵坐标为-3，试求出a的值；
（2）求a的取值范围；
（3）若点P的横、纵坐标都是整数，试求出a的值以及P点的坐标.
已知某正数的两个平方根分别是a+3和2a-15,b的立方根是-2，求3a+b的算术平方根.
（1）计算：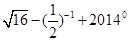
；（2）求
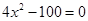中x的值．
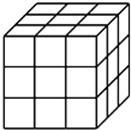
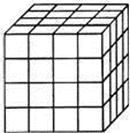
将一个正方体表面全部涂上颜色
把正方体的棱三等分，然后沿等分线把正方体切开，得到27个小正方体，我们把仅有i个面涂色的小正方体的个数记为
，例如：通过观察我们可以发现仅有3个面涂色的小正方体个数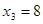
，仅有2个面涂色的小正方体个数
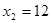，仅有1个面涂色的小正方体个数
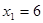，6个面均不涂色的小正方体个数
；
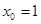（1）如果把正方体的棱四等分，同样沿等分线把正方体切开，得到64个小正方体，那么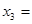
________，
_______，
_______，
_________；
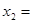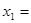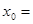（2）如果把正方体的棱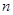
等分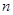（大于3），然后沿等分线把正方体切开，得到
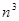个小正方体，且满足
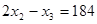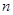，请求出的值.
