(·辽宁葫芦岛)如图,小岛A在港口B的北偏东50°方向,小岛C在港口B的北偏西25°方向,一艘轮船以每小时20海里的速度从港口B出发向小岛A航行,经过5小时到达小岛A,这时测得小岛C在小岛A的北偏西70°方向,求小岛A距离小岛C有多少海里?(最后结果精确到1海里,参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
(·辽宁沈阳)我国是世界上严重缺失的国家之一,全国总用水量逐年上升,全国总用水量可分为农业用水量、工业用水量和生活用水量三部分.为了合理利用水资源,我国连续多年对水资源的利用情况进行跟踪调查,将所得数据进行处理,绘制了2008年全国总用水量分布情况扇形统计图和2004﹣2008年全国生活用水量折线统计图的一部分如下:
(1)2007年全国生活用水量比2004年增加了16%,则2004年全国生活用水量为 亿m3,2008年全国生活用水量比2004年增加了20%,则2008年全国生活用水量为 亿m3;
(2)根据以上信息,请直接在答题卡上补全折线统计图;
(3)根据以上信息2008年全国总水量为 亿;
(4)我国2008年水资源总量约为2.75×104亿m3,根据国外的经验,一个国家当年的全国总用水量超过这个国家年水资源总量的20%,就有可能发生“水危机”.依据这个标准,2008年我国是否属于可能发生“水危机”的行列?并说明理由.
(·辽宁丹东)一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P (x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
(·辽宁丹东)某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的) ,并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有2000名学生,请估计该校喜爱电视剧节目的人数.
(·辽宁大连)某地区共有1800名初三学生,为解决这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.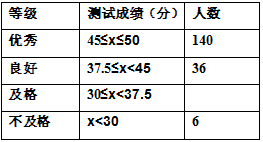
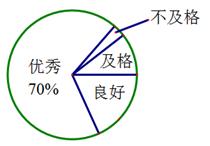
根据以上信息,解答下列问题:(1)本次测试学生体质健康成绩为良好的有_________人,达到优秀的人数占本次测试人数的百分比为____%.
本次测试学生人数为_________人,其中,体质健康成绩为及格的有________人,不及格的人数占本次测试总人数的百分比是__________%.
试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.