如图,在每一个四边形ABCD中,均有AD//BC,CD⊥BC∠ABC=60°,AD=8,BC=12.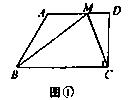
(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为__________;
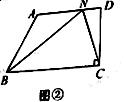
(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;
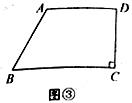
(3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC的值最小?若存在,求出此时
cos∠BPC的值;若不存在,请说明理由。
已知抛物线y=ax2+x+2.当a=-1时,求此抛物线的顶点坐标和对称轴
若代数式-x2+x+2的值为正整数,求x的值;
若a是负数时,当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0). 若点M在点N的左边,试比较a1与a2的大小.
数学课上,同学们探究发现:如图1,顶角为36°的等腰三角形具有一种特性,即经过它某一顶点的一条直线可把它分成两个小等腰三角形. 并且对其进行了证明.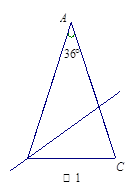
证明后,小乔又发现:下面两个等腰三角形如图2、图3也具有这种特性.请你在
图2、图3中分别画出一条直线,把它们分成两个小等腰三角形,并在图中标出所画等腰三角形两个底角的度数;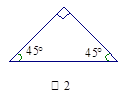

接着,小乔又发现:直角三角形和一些非等腰三角形也具有这样的特性,如:直角三角形斜边上的中线可以把它分成两个小等腰三角形.请你画出一个具有这种特性的三角形的示意图,并在图中标出此三角形的各内角的度数.(说明:要求画出的既不是等腰三角形,也不是直角三角形.)
甲学校到丙学校要经过乙学校. 从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径.点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.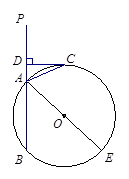
求证:CD为⊙O的切线;
若DC+DA=6,⊙O的直径为10,求AB的长.
已知:如图,四边形ABCD中,BC=CD=DB,∠ADB=90°,sin∠ABD= ,S△BCD=
,S△BCD=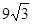 . 求四边形ABCD的周长.
. 求四边形ABCD的周长.