小明解方程 ﹣
﹣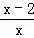 =1的过程如图.请指出他解答过程中的错误,并写出正确的解答过程.
=1的过程如图.请指出他解答过程中的错误,并写出正确的解答过程.
因式分解: .
.
如图,在数轴上点A、B、C表示的数分别为-2,1,6,点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)则AB= ,BC= ,AC= ;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动。请问:BC-AB的值是否随着运动时间t的变化而改变?若变化,请说明理由;若不变,请求其值;
(3)由第(1)小题可以发现,AB+BC=AC.若点C以每秒3个单位长度的速度向左运动,同时,点A和点B分别以每秒1个单位长度和每秒2个单位长度的速度向右运动.请问:当运动时间t在0~1秒之间时,AB、BC、AC之间是否存在类似于(1)的数量关系?请说明理由.
如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a、b、c,其中a、b是直角边.正方形的边长分别是a、b.
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一: ;方法二: ;
(2)观察图②,试写出 ,
, ,2ab,
,2ab, 这四个代数式之间的等量关系;
这四个代数式之间的等量关系;
(3)请利用(2)中等量关系解决问题:
已知图①中一个三角形面积是6,图②的大正方形面积是49,求 +
+ 的值.
的值.
(4)利用你发现的结论,求: 的值.
的值.
如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
(1)B→D( , ),,C→ (-3,-4);
(2)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-1,-2),请在图中标出妮妮的位置E点.
(3)在(3)中贝贝若每走1m需消耗1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
定义一种新运算:观察下列各式:1⊙3=1×4+3=7 ;3⊙(-1)= 3×4-1=11;5⊙4="5×4+4=24" ;4⊙(-3)= 4×4-3=13
(1)请你想一想:用代数式表示a⊙b的结果为:___________;
(2)若a≠b,那么a⊙b______b⊙a(填入“=”或“≠ ”);
(3)若a⊙(-2b)= 4,请计算(a-b)⊙(2a+b)的值.