QQ先生的鱼缸中有7条鱼，其中6条青鱼和1条黑鱼，计划从当天开始，每天中午从该鱼缸中抓出1条鱼（每条鱼被抓到的概率相同）并吃掉．若黑鱼未被抓出，则它每晚要吃掉1条青鱼（规定青鱼不吃鱼）．
（Ⅰ）求这7条鱼中至少有6条被QQ先生吃掉的概率；
（Ⅱ）以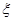
表示这7条鱼中被QQ先生吃掉的鱼的条数，求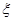的分布列及其数学期望
．
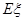（本小题满分12分） 已知数列
为等差数列，且
，
．
(1) 求数列的通项公式； (2) 令
，求证：数列
是等比数列．
（3）令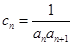
，求数列
的前
项和
.
(本题满分10分)选修4—5：不等式选讲
若关于x的不等式
恒成立，求a的取值范围．
(本题满分10分)选修4—4：坐标系与参数方程
已知直线
的极坐标方程为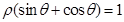
，曲线
的参数方程为
（
为参数）．
（Ⅰ）求直线的直角坐标方程；
（Ⅱ）设直线与曲线交于A，B两点，原点为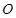
，求
的面积．
(本题满分10分)选修4—1：几何证明选讲已知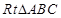
中，
，
，
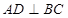垂足为D，
，垂足为F，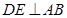
，垂足为E．
求证：（Ⅰ）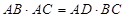
；
（Ⅱ）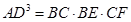
已知函数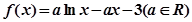
（1）当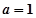
时，求函数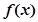
的单调区间；
（2）若函数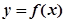
的图像在点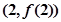
处的切线的倾斜角为
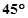，问：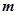
在什么范围取值时，对于任意的
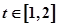，函数
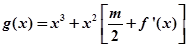在区间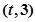
上总存在极值？