调查1000名50岁以上有吸烟习惯与患慢性气管炎的人的情况,获数据如下表:
| |
患慢性气管炎 |
未患慢性气管炎 |
总计 |
| 吸烟 |
360 |
320 |
680 |
| 不吸烟 |
140 |
180 |
320 |
| 合计 |
500 |
500 |
1000 |
试问:根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为吸烟习惯与患慢性气管炎病有关?参考数据如下:
(k=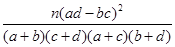 ,且P(K2≥6.635)≈0.01,)
,且P(K2≥6.635)≈0.01,)
已知数列 是等差数列,
是等差数列,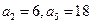 ;数列
;数列 的前n项和是
的前n项和是 ,且
,且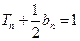 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证:数列 是等比数列;
是等比数列;
(3)记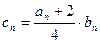 ,求
,求 的前n项和
的前n项和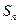
某厂用甲、乙两种原料生产A、B两种产品,已知生产1吨A产品,1吨B产品分别需要的甲、乙原料数,可获得的利润数及该厂现有原料数如下表所示.问:在现有原料下,A、B产品应各生产多少才能使利润总额最大?利润总额最大是多少?列产品和原料关系表如下:

|
A产品 (1吨) |
B产品 (1吨) |
总原料 (吨) |
||
| 甲原料(吨) |
2 |
5 |
10 |
||
| 乙原料(吨) |
6 |
3 |
18 |
||
| 利润(万元) |
4 |
3 |
如图,甲船在A处观察乙船,乙船在它的北偏东60°的方向,两船相距a海里,乙船正向北行驶,若甲船是乙船速度的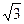 倍,问:甲船应取什么方向才能追上乙船?追上时甲船行驶了多少海里?
倍,问:甲船应取什么方向才能追上乙船?追上时甲船行驶了多少海里?
(本小题12分)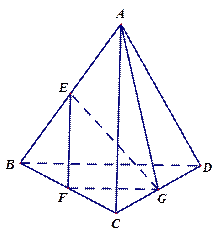
四面体 中,
中, ,
, 分别是
分别是 的中点,且
的中点,且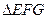 为正三角形,
为正三角形,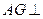 平面
平面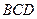 .
.
①求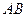 与平面
与平面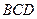 所成角的大小;
所成角的大小;
②求二面角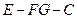 的平面角的余弦值.
的平面角的余弦值.
(本小题12分)
四棱锥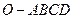 中,
中, 底面
底面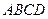 ,且
,且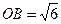 ,底面
,底面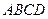 是菱形;点
是菱形;点 在平面
在平面 内的射影
内的射影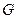 恰为
恰为 的重心.
的重心.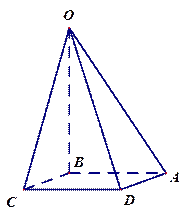 ①求
①求 的长;
的长;
②求二面角 的平面角的余弦值.
的平面角的余弦值.