如图 ,梯形
,梯形 中,
中,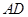 ∥
∥ ,
, ,
,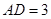 ,
,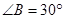 .动点
.动点 从点
从点 出发,以每秒
出发,以每秒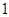 个单位长度的速度在线段
个单位长度的速度在线段 上运动;动点
上运动;动点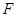 同时从点
同时从点 出发,以每秒
出发,以每秒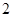 个单位长度的速度在线段
个单位长度的速度在线段 上运动.以
上运动.以 为边作等边△
为边作等边△ ,与梯形
,与梯形 在线段
在线段 的同侧.设点
的同侧.设点 、
、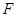 运动时间为
运动时间为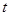 ,当点
,当点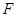 到达
到达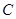 点时,运动结束.
点时,运动结束.
(1)当等边△ 的边
的边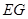 恰好经过点
恰好经过点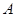 时,求运动时间
时,求运动时间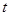 的值;
的值;
(2)在整个运动过程中,设等边△ 与梯形
与梯形 的重合部分面积为
的重合部分面积为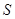 ,请直接写出
,请直接写出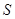 与
与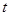 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量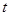 的取值范围;
的取值范围;
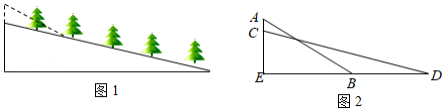
(3)如图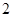 ,当点
,当点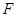 到达
到达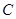 点时,将等边△
点时,将等边△ 绕点
绕点 旋转
旋转 (
( ),
),
直线 分别与直线
分别与直线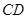 、直线
、直线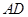 交于点
交于点 、
、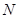 .是否存在这样的
.是否存在这样的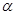 ,使△
,使△ 为等腰三角形?若存在,请求出此时线段
为等腰三角形?若存在,请求出此时线段 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
如图所示,有一个可以自由转动的转盘,其盘面分为4等份,在每一等份分别标有对应的数字2,3,4,5.小明打算自由转动转盘10次,现已经转动了8次,每一次停止后,小明将指针所指数字记录如下:
|
次数 |
第1次 |
第2次 |
第3次 |
第4次 |
第5次 |
第6次 |
第7次 |
第8次 |
第9次 |
第10次 |
|
数字 |
3 |
5 |
2 |
3 |
3 |
4 |
3 |
5 |
(1)求前8次的指针所指数字的平均数.
(2)小明继续自由转动转盘2次,判断是否可能发生“这10次的指针所指数字的平均数不小于3.3,且不大于3.5”的结果?若有可能,计算发生此结果的概率,并写出计算过程;若不可能,说明理由.(指针指向盘面等分线时为无效转次.
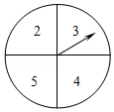
自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .求斜坡 的长.(结果保留根号)
已知关于 , 的二元一次方程组 的解满足 ,求 的取值范围.
(1)方法选择
如图①,四边形 是 的内接四边形,连接 , , .求证: .
小颖认为可用截长法证明:在 上截取 ,连接
小军认为可用补短法证明:延长 至点 ,使得
请你选择一种方法证明.
(2)类比探究
[探究1]
如图②,四边形 是 的内接四边形,连接 , , 是 的直径, .试用等式表示线段 , , 之间的数量关系,并证明你的结论.
[探究2]
如图③,四边形 是 的内接四边形,连接 , .若 是 的直径, ,则线段 , , 之间的等量关系式是 .
(3)拓展猜想
如图④,四边形 是 的内接四边形,连接 , .若 是 的直径, ,则线段 , , 之间的等量关系式是 .

如图,在正方形 中, , 为对角线 上一动点,连接 , ,过 点作 ,交直线 于点 . 点从 点出发,沿着 方向以每秒 的速度运动,当点 与点 重合时,运动停止.设 的面积为 , 点的运动时间为 秒.
(1)求证: ;
(2)求 与 之间关系的函数表达式,并写出自变量 的取值范围;
(3)求 面积的最大值.