如图，在
中，
，
，
，
分别是边
的中点，点
从点
出发沿
方向运动，过点作
于
，过点作
交
于
，当点与点
重合时，点停止运动．设
，
．
（1）求点到
的距离
的长；
（2）求
关于
的函数关系式（不要求写出自变量的取值范围）；
（3）是否存在点，使
为等腰三角形？若存在，请求出所有满足要求的的值；若不存在，请说明理由．
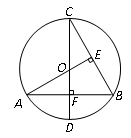
如图，扇形OAB的半径为4，圆心角∠AOB=90°，点C是
上异于点A、B的一动点，过点C作CD⊥OB于点D，作CE⊥OA于点E，联结DE，过O点作OF⊥DE于点F，点M为线段OD上一动点，联结MF，过点F作NF⊥MF，交OA于点N．
（1）当
时，求
的值；
（2）设OM=x，ON=y，当
时，求y关于x 的函数解析式，并写出它的定义域；
（3）在（2）的条件下，联结CF，当△ECF与△OFN相似时，求OD的长．
已知：如图，在平面直角坐标系xOy中，直线
与x轴、y轴分别交于点A、B，点C在线段AB上，且
．
（1）求点C的坐标（用含有m的代数式表示）；
（2）将△AOC沿x轴翻折，当点C的对应点C′恰好落在抛物线
上时，求该抛物线的表达式；
（3）设点M为（2）中所求抛物线上一点，当以A、O、C、M为顶点的四边形为平行四边形时，请直接写出所有满足条件的点M的坐标．
已知：如图，在□ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC．
（1）求证：BE=DG；
（2）若∠BCD=120°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？证明你的结论．
某文具店店主到批发中心选购甲、乙两种品牌的文具盒，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．
（1）求y关于x的函数解析式（不必写出自变量x的取值范围）；
（2）该店主用3000元选购了甲品牌的文具盒，用同样的钱选购了乙品牌的文具盒，乙品牌文具盒的单价比甲品牌的单价贵15元，求所选购的甲、乙文具盒的数量．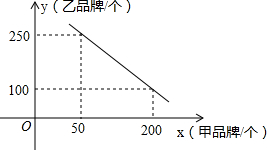
如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，BC=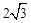
.
（1）求AB的长；
（2）求⊙O的半径．