函数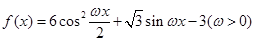
在一个周期内的图象如图所示，
为图象的最高点，
、
为图象与
轴的交点，且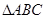
为正三角形。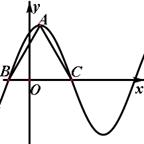
（Ⅰ）求
的值及函数
的值域；
（Ⅱ）若
，且
，求
的值。
已知圆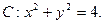
（1）直线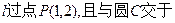
A、B两点，若
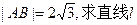的方程；
（2）过圆C上一动点M作平行于x轴的直线m，设m与y轴的交点为N，若向量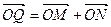
，求动点Q的轨迹方程，并说明此轨迹是什么曲线。
(12分)如图，直三棱柱ABC—A1B1C1的底面是等腰直角三角形，∠A1C1B1=90°，A1C1=1，AA1=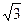
，D是线段A1B1的中点．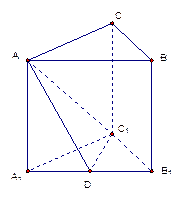
（1）证明：面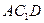
⊥平面A1B1BA；
（2）证明：
；
（3）求棱柱ABC—A1B1C1被平面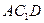分成两部分的体积比．
设函数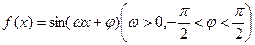
给出下列四个论断：
①它的周期为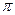
；
②它的图象关于直线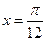
对称；
③它的图象关于点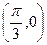
对称；④在区间
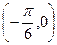上是增函数。
请以其中两个论断为条件，另两个为结论，写出一个正确的命题： .（用符号表示）
已知椭圆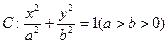
过点
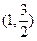，且离心率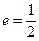
。
（Ⅰ）求椭圆方程；
（Ⅱ）若直线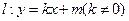
与椭圆交于不同的两点
、
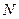，且线段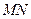
的垂直平分线过定点
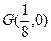，求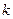
的取值范围。
(12分)某银行准备新设一种定期存款业务，经预测，存款量与存款利率的平方成正比，比例系数为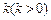
，且知当利率为0.012时，存款量为1.44亿；又贷款的利率为
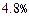时，银行吸收的存款能全部放贷出去；若设存款的利率为
，
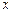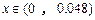;试写出存款量f(x)与存款利率的关系式，且当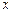为多少时，银行可获得最大收益？