三名大学生竞选系学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，如表一和图一：
表一

	A	B	C
笔试	85	95	90
口试		80	85

 

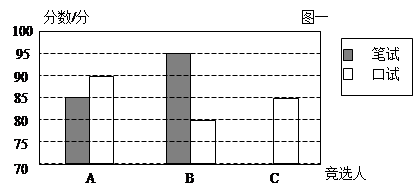
（1）请将表一和图一中的空缺部分补充完整．
（2）竞选的最后一个程序是由本系的300名学生进行投票，三位候选人的得票情况如图二（没有弃权票，每名学生只能推荐一个），请计算每人的得票数．

（3）若每票计1分，系里将笔试、口试、得票三项测试得分按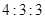的比例确定个人成绩，请计算三位候选人的最后成绩，并根据成绩判断谁能当选．

科目 数学   题型 解答题   难度 中等

知识点： 统计量的选择