A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.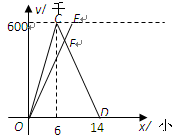
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶7了小时时,两车相遇,求乙车速度.
解方程: 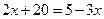
在广州亚运会中,志愿者们手上、脖子上的丝巾非常美丽.车间70名工人承接了制作丝巾的任务,已知每人每天平均生产手上的丝巾1 800条或者脖子的丝巾1 200条,一条脖子上的丝巾要配两条手上的丝巾.为了使每天生产的丝巾刚好配套,应分配多少名工人生产脖子上的丝巾,多少名工人生产手上的丝巾?
用同样规格的黑白两种颜色的正方形,按如图的方式拼图,请根据图中的信息完成下列的问题.
(1)在图②中用了块黑色正方形,在图③中用了块黑色正方形;
(2)按如图的规律继续铺下去,那么第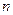 个图形要用块黑色正方形;
个图形要用块黑色正方形;
(3)如果有足够多的白色正方形,能不能恰好用完90块黑色正方形,拼出具有以上规律的图形?如果可以请说明它是第几个图形;如果不能,说明你的理由.
如图, 一艘客轮沿东北方向OC行驶,在海上O处发现灯塔A在北偏西30°方向上, 灯塔B在南偏东60°方向上.
(1)在图中画出射线OA、OB、OC;
(2)求∠AOC与∠BOC的度数,你发现了什么?
如图,已知 ,
, ,
, ,求
,求 的长
的长