A. [选修4-1:几何证明选讲](本小题满分10分)
如图,AB是⊙O的直径,C是⊙O外一点,且AC=AB,BC交⊙O于点D.
已知BC=4,AD=6,AC交⊙O于点E,求四边形ABDE的周长.
如图,设抛物线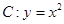 的焦点为
的焦点为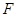 ,动点
,动点 在直线
在直线 上
上
运动,过P作抛物线C的两条切线PA,PB,且与抛物线C分别相切于A,B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.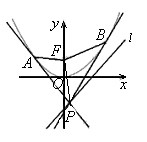
已知正方形ABCD的边长为2, ,
,
将正方形ABCD沿对角线BD折起,使 ,得到三棱锥
,得到三棱锥 ,如图所示。
,如图所示。
(1)当a=2时,求证: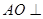 平面BCD;
平面BCD;
(2)当二面角 的大小为
的大小为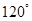 时,
时,
求二面角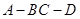 的正切值。
的正切值。
有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出 的分布列,求
的分布列,求 的数学期望。
的数学期望。
已知等差数列 的前n项和为
的前n项和为 ,首项
,首项 ,公差
,公差 ,且
,且 成等比数列。
成等比数列。
(1)求数列 的通项公式及
的通项公式及 ;
;
(2)记 =
= +
+ +
+ +…+
+…+ ,
,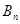 =
= +
+ 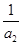 +
+ +… +
+… +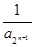 ,
,
当n≥2时,试比较 与
与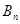 的大小。
的大小。
设函数 .
.
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)若关于x的方程 有三个不同实根,求实数
有三个不同实根,求实数 的取值范围;
的取值范围;
(3)已知当 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。