(1)如图一,等边△ABC中,D是AB上的动点,以CD为一边,向上作等边△EDC,连结AE。求证:AE//BC;
(2)如图二,将(1)中等边△ABC的形状改成以BC为底边的等腰三角形。所作△EDC改成相似于△ABC。请问:是否仍有AE//BC?证明你的结论。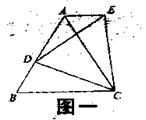

(每题各6分,共12分)
(1) 解不等式组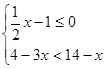 并将其解集在数轴上表示出来。
并将其解集在数轴上表示出来。
(2)当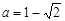 时,求
时,求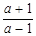 -
-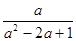 ÷
÷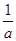 的值.
的值.
如图,在平面直角坐标系中,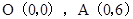 ,
,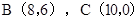 ,点Q从点A出发以1cm/s的速度向点B运动,点P从点O出发以2cm/s的速度在线段OC间往返运动,P、Q两点同时出发,当点Q到达点B时,两点同时停止运动.
,点Q从点A出发以1cm/s的速度向点B运动,点P从点O出发以2cm/s的速度在线段OC间往返运动,P、Q两点同时出发,当点Q到达点B时,两点同时停止运动.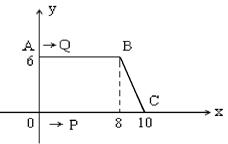
(1)当运动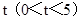 秒时,
秒时,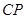 =____________,
=____________,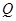 的坐标是( ____ , ____ )(用含t的代数式表示)
的坐标是( ____ , ____ )(用含t的代数式表示)
(2)当t为何值时,四边形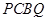 的面积为36cm2?
的面积为36cm2?
(3)当t为何值时,四边形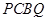 为平行四边形?
为平行四边形?
(4)当t为何值时,四边形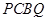 为等腰梯形?
为等腰梯形?
在平面直角坐标系中,点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度.
| P从点O出发 平移次数 |
可能到达的 点的坐标 |
| 1 次 |
(0,2)(1,0) |
| 2 次 |
|
| 3 次 |
实验操作
在平面直角坐标系中描出点P从点O出发,平移1次后,2次后,3次后可能到达的点,并把相应点的坐标填写在表格中.
观察思考
任一次平移,点P可能到达的点在我们学过的一次函数的图像上,如:平移1次后点P在函数________________的图像上;平移2次后点P在函数_________________的图像上
(3)规律发现
由此我们知道,平移n次后点P在函数__________________的图像上(请填写相应的解析式)
“职来职往”中各家企业对A、B、C三名应聘者进行了面试、语言交际和专业技能共三项素质测试,他们的成
绩如下表所示:
 应聘者 应聘者 得分 得分测试项目 |
A |
B |
C |
| 面试 |
72 |
56 |
48 |
| 语言交际 |
88 |
80 |
88 |
| 专业技能 |
64 |
72 |
80 |
(1)如果根据三项测试的平均成绩确定录用人员,你选择谁?请说明理由;
(2)根据实际需要,新浪微博公司给出了选人标准:将面试、语言交际和专业技能三项测试得分按1:3:4比例确定各人的测试成绩,你选谁?请说明理由.
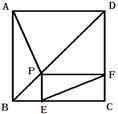
如图,正方形ABCD中,P为对角线BD上一点(P点不与B、D重合),PE⊥BC于E,PF⊥DC于F,连接EF,猜想AP与EF的关系并证明你的结论.