在梯形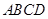 中,
中,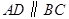 ,
,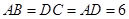 ,
,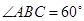 ,点
,点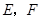 分别在线段
分别在线段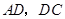 上(点
上(点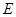 与点
与点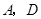 不重合),且
不重合),且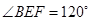 ,设
,设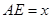 ,
,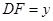 .
.
(1)求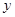 与
与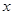 的函数表达式;
的函数表达式;
(2)当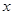 为何值时,
为何值时,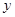 有最大值,最大值是多少?
有最大值,最大值是多少?
如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC•CD=CP•BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.
一次函数 与反比例函数
与反比例函数 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤衫商店共获利多少元?
如图,抛物线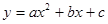 (
(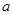 ≠0)与
≠0)与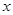 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与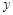 轴交与点C(0,2).
轴交与点C(0,2).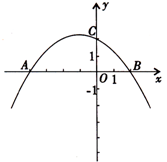
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;(解题用图见答题卡)
(3)以AB为直径作⊙M,直线经过点E(-1,-5),并且与⊙M相切,求该直线的解析式.(解题用图见答题卡)
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD—AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.