如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=1200.
(I)求证:平面ADE⊥平面ABE ;
(II)求二面角A—EB—D的大小的余弦值.
(本小题满分13分)为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
(1)求实数 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数;
(2)若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生自不同组的概率.
已知函数
(1)求函数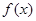 的最小值及单调减区间;
的最小值及单调减区间;
(2)在
 中,
中,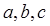 分别是角
分别是角 的对边,且
的对边,且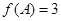 ,
,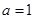 ,
, ,且
,且 ,求
,求 ,c的值
,c的值
(本小题满分13分)已知等比数列 满足
满足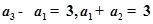 .
.
(1)求数列 的前15项的和
的前15项的和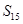 ;
;
(2)若等差数列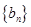 满足
满足 ,
, ,求数列
,求数列 的前
的前 项的和
项的和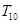
如图,在三棱锥 中,
中, ,
, ,
, °,平面
°,平面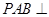 平面
平面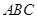 ,
,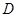 、
、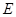 分别为
分别为 、
、 中点.
中点.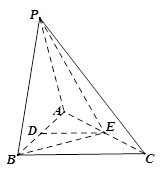
(1)求证: ∥平面
∥平面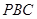 ;
;
(2)求证: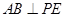 ;
;
(3)求二面角 的大小.
的大小.
在2012年“双节”期间,高速公路车辆较多。某调查公司在一服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取了40名驾驶员进行调查,将他们在某段高速公路上的车速(km/t)分成6段: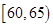 ,
, ,
,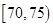 ,
, ,
, ,
,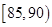 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
(1)该公司在调查取样中,用到的是什么抽样方法?
(2)求这40辆小型汽车车速的众数和中位数的估计值;
(3)若从车速在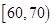 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 中的车辆数
中的车辆数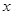 的分布列及其数学期望。
的分布列及其数学期望。