在2012年“双节”期间,高速公路车辆较多。某调查公司在一服务区从七座以下小型汽车中,按进服务区的先后每间隔50辆就抽取一辆的抽样方法,抽取了40名驾驶员进行调查,将他们在某段高速公路上的车速(km/t)分成6段: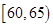 ,
, ,
,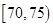 ,
, ,
, ,
,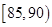 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问:
(1)该公司在调查取样中,用到的是什么抽样方法?
(2)求这40辆小型汽车车速的众数和中位数的估计值;
(3)若从车速在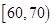 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在 中的车辆数
中的车辆数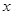 的分布列及其数学期望。
的分布列及其数学期望。
(本小题满分14分)
已知直角梯形 中(如图1),
中(如图1),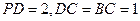 ,
,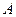 为
为 的中点,
的中点,
将 沿
沿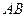 折起,使面
折起,使面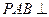 面
面 (如图2),点
(如图2),点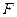 在线段
在线段 上,
上,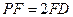 .
.
(1)求异面直线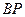 与
与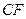 所成角的余弦值;
所成角的余弦值;
(2)求二面角 的余弦值;
的余弦值; (3)在四棱锥
(3)在四棱锥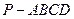 的棱
的棱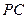 上是否存在一点
上是否存在一点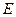 ,使得
,使得 平面
平面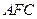 ,若存在,求出
,若存在,求出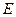 点的位置,若不存在,请说明理由.
点的位置,若不存在,请说明理由.
(本小题共14分)
某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、
B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如下表: 如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
(本小题满分12分)
在 中,角
中,角 所对的边长分别为
所对的边长分别为 ,
, ,
,  ,
, 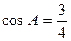 ,(1)求
,(1)求 的值;(2)求
的值;(2)求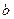 的值.
的值.
(本小题满分12分)
已知命题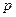 :关于
:关于 的方程
的方程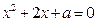 有实数解,命题
有实数解,命题 :关于
:关于 的不等式
的不等式 的解集为
的解集为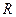 ,若
,若 是真命题,求实数
是真命题,求实数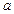 的取值范围.
的取值范围.
(本小题满分14分)
已知函数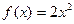 ,
,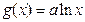 (
(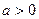 ).
).
(1)当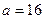 时,试求函数
时,试求函数 在
在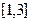 上的值域;
上的值域;
(2)若直线 交
交 的图象
的图象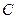 于
于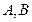 两点,与
两点,与 平行的另一直线
平行的另一直线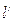 与图象
与图象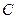 切于点
切于点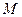 .
.
求证: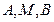 三点的横坐标成等差数
三点的横坐标成等差数 列;
列;