如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点.
(1)直接写出点A的坐标，并求出抛物线的解析式；
(2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E
①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?
②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t值.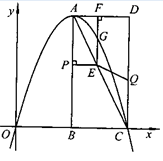
已知关于x的一元二次方程x2+mx+n=0的一个解是2,另一个解是正数, 而且也是方程(x+4)2-52=3x的解,你能求出m和n的值吗?
用适当的方法解下列一元二次方程.(每小题5分,共15分)
(1)5x(x-3)="6-2x;" (2)3y2+1=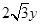
;(3)(x-a)2=1-2a+a2(a是常数)
一商店1月份的利润是2500元，3月份的利润达到3025元，这两个月的利润平均月增长的百分率是多少？
已知关于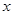
的方程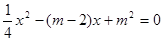
⑴若方程有两个相等的实数根,求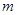
的值,并求出此时方程的根
⑵是否存在正数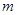,使方程的两个实数根的平方和等于224 ？若存在,求出满足条件的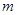的值； 若不存在，请说明理由。
试证明：不论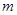
为何值，方程
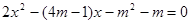总有两个不相等的实数根。