某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为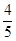 ,第二、第三种
,第二、第三种
产品受欢迎的概率分别为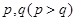 ,且不同种产品是否受欢迎相互独立.记
,且不同种产品是否受欢迎相互独立.记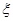 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
 |
(Ⅰ)求该公司至少有一种产品受欢迎的概率;
(Ⅱ)求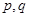 的值;
的值;
(Ⅲ)求数学期望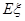 .
.
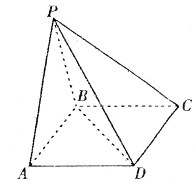
如图,四棱锥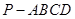 的底面
的底面 是矩形,
是矩形,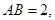
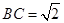 ,且侧面
,且侧面 是正三角形,平面
是正三角形,平面 平面
平面 ,
,
(Ⅰ)求证: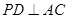 ;
;
(Ⅱ)在棱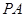 上是否存在一点
上是否存在一点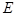 ,使得二面角
,使得二面角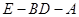 的大小为45°.若存在,试求
的大小为45°.若存在,试求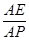 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
已知函数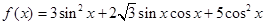 .
.
(1)若 ,求
,求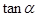 的值;
的值;
(2)设△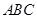 三内角
三内角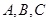 所对边分别为
所对边分别为 且
且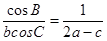 ,求
,求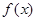 在
在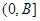 上的值域.
上的值域.
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明: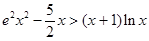
已知中心在原点O,焦点F1、F2在x轴上的椭圆E经过点C(2,2),且抛物线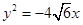 的焦点为F1.
的焦点为F1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)垂直于OC的直线l与椭圆E交于A、B两点,当以AB为直径的圆P与y轴相切时,求直线l的方程和圆P的方程.