如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.

(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
在等差数列{an}中,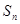 为其前n项和
为其前n项和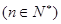 ,且
,且
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设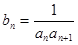 ,求数列
,求数列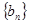 的前
的前 项和
项和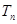 .
.
已知函数 ,
, ,且
,且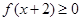 的解集为
的解集为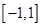 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若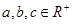 ,且
,且 ,求证:
,求证: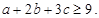
已知曲线 的参数方程是
的参数方程是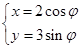 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线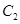 的极坐标方程是ρ=2,正方形ABCD的顶点都在
的极坐标方程是ρ=2,正方形ABCD的顶点都在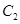 上,且A,B,C,D依逆时针次序排列,点A的极坐标为
上,且A,B,C,D依逆时针次序排列,点A的极坐标为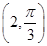 .
.
(Ⅰ)求点A,B,C,D的直角坐标;
(Ⅱ)设P为 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
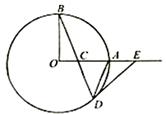
如图, 、
、 是圆
是圆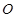 的半径,且
的半径,且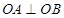 ,
, 是半径
是半径 上一点:延长
上一点:延长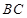 交圆
交圆 于点
于点 ,过
,过 作圆
作圆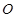 的切线交
的切线交 的延长线于点
的延长线于点 .求证:
.求证: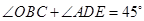 .
.
已知函数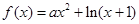 .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,不等式
时,不等式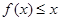 恒成立,求实数
恒成立,求实数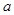 的取值范围.
的取值范围.
(Ⅲ)求证: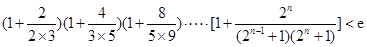 (
(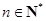 ,e是自然对数的底数).
,e是自然对数的底数).