某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组[13, 14)；第二组[14, 15)，……，第五组[17, 18]. 下图是按上述分组方法得到的频率分布直方图.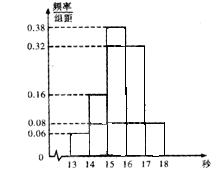
(1)若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；
(2)设m、n表示该班某两位同学的百米测试成绩，且已知m, n∈[13, 14)∪[17, 18]. 求事件“|m－n|>1”的概率.
（本小题满分12分）
已知函数
论函数
的奇偶性，并说明理由．
某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现在采用分层抽样法（层内采用不放回的简单随机抽样）从甲，乙两组中共抽取3人进行技术考核.
（1）求甲，乙两组各抽取的人数；
（2）求从甲组抽取的工人中恰有1名女工的概率；
（3）令X表示抽取的3名工人中男工人的人数，求X的分布列及数学期望．
已知函数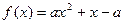
（
）
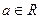(1)若函数
有最大值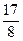
，求实数a的值； (2)解不等式
(a∈R)．
（本小题满分12分）
已知命题
,命题
,
若命题
是真命题,求实数a的取值范围.
（本小题满分12分）
已知集合A＝{x/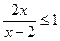
}，集合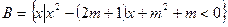
(1)求集合A， B； (2) 若B⊆A，求m的取值范围．