(本小题满分14分)
(1)若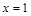 是
是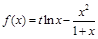 的一个极值点,求
的一个极值点,求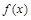 的单调区间;
的单调区间;
(2)证明:若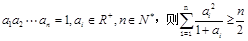 ;
;
(3)证明:若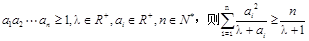 .
.
(本小题满分13分)已知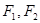 为椭圆
为椭圆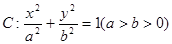 的左,右焦点,
的左,右焦点,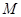 为椭圆上的动点,且
为椭圆上的动点,且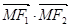 的最大值为1,最小值为-2.
的最大值为1,最小值为-2.
(1)求椭圆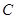 的方程;
的方程;
(2)过点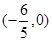 作不与y轴垂直的直线
作不与y轴垂直的直线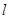 交该椭圆于
交该椭圆于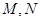 两点, A为椭圆的左顶点.试判断
两点, A为椭圆的左顶点.试判断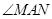 是否为直角,并说明理由.
是否为直角,并说明理由.
(本小题满分12分)在淘宝网上,某店铺专卖孝感某种特产.由以往的经验表明,不考虑其他因素,该特产每日的销售量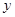 (单位:千克)与销售价格
(单位:千克)与销售价格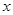 (单位:元/千克,
(单位:元/千克,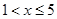 )满足:当
)满足:当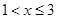 时,
时,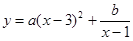 ,
,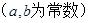 ;当
;当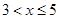 时,
时,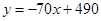 .已知当销售价格为
.已知当销售价格为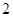 元/千克时,每日可售出该特产600千克;当销售价格为
元/千克时,每日可售出该特产600千克;当销售价格为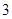 元/千克时,每日可售出150千克.
元/千克时,每日可售出150千克.
(1)求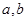 的值,并确定
的值,并确定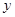 关于
关于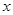 的函数解析式;
的函数解析式;
(2)若该特产的销售成本为 元/千克,试确定销售价格
元/千克,试确定销售价格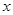 的值,使店铺每日销售该特产所获利润
的值,使店铺每日销售该特产所获利润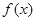 最大(
最大(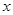 精确到0.1元/千克).
精确到0.1元/千克).
(本小题满分12分)设数列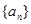 的前
的前 项和为
项和为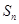 ,点
,点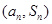 在直线
在直线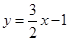 上.
上.
(1)求数列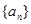 的通项公式;
的通项公式;
(2)在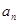 与
与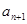 之间插入
之间插入 个数,使这
个数,使这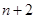 个数组成公差为
个数组成公差为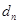 的等差数列,求数列
的等差数列,求数列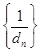 的前
的前 项和
项和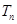 ,并求使
,并求使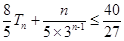 成立的正整数
成立的正整数 的最大值.
的最大值.
(本小题满分12分)在△ABC中,a,b,c分别为内角A,B,C的对边, 面积
(1)求角C的大小;
(2)设函数 ,求
,求 的最大值,及取得最大值时角B的值.
的最大值,及取得最大值时角B的值.