一个三棱柱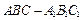 直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设 、
、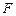 分别为
分别为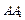 和
和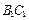 的中点.
的中点.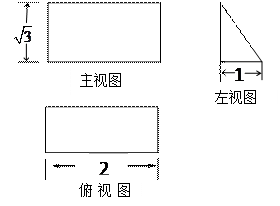
(Ⅰ)求几何体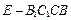 的体积;
的体积;
(Ⅱ)证明: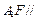 平面
平面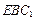 ;
;
(Ⅲ)证明:平面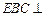 平面
平面 .
.
选修4-1:几何证明选讲
如图,点 在圆
在圆 直径
直径 的延长线上,
的延长线上,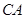 切圆
切圆 于
于 点,
点, 的平分线
的平分线 交
交 于点
于点 ,交
,交 于
于 点.
点.
(1)求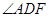 的度数;
的度数;
(2)若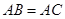 ,求
,求 .
.
已知函数 ,
,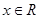 , 其中,
, 其中,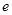 是自然对数的底数.函数
是自然对数的底数.函数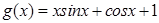 ,
,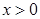 .
.
(Ⅰ)求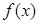 的最小值;
的最小值;
(Ⅱ)将 的全部零点按照从小到大的顺序排成数列
的全部零点按照从小到大的顺序排成数列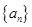 ,求证:
,求证:
(1)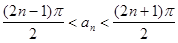 ,其中
,其中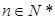 ;
;
(2) .
.
已知如图,圆 和抛物线
和抛物线 ,圆的切线
,圆的切线 与抛物线
与抛物线 交于不同的点
交于不同的点 ,
, .
.
(1)当直线 的斜率为
的斜率为 时,求线段
时,求线段 的长;
的长;
(2)设点 和点
和点 关于直线
关于直线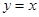 对称,问是否存在圆的切线
对称,问是否存在圆的切线 使得
使得 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
如图,在四棱锥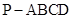 中,侧棱
中,侧棱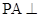 底面
底面 ,
,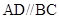 ,
, ,
,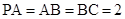 ,
,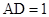 ,
, 是棱
是棱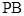 中点.
中点.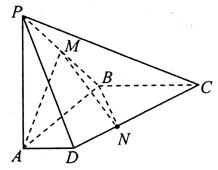
(1)求证: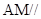 平面
平面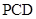 ;
;
(2)设点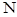 是线段
是线段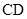 上一动点,且
上一动点,且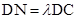 ,当直线
,当直线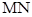 与平面
与平面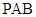 所成的角最大时,求
所成的角最大时,求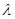 的值.
的值.
某市规定,高中学生三年在校期间参加不少于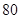 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段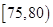 ,
, ,
,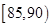 ,
,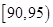 ,
, (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(1)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(2)从全市高中学生(人数很多)中任意选取3位学生,记 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 的分布列和数学期望
的分布列和数学期望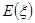 .
.