选修4-1:几何证明选讲
如图,点 在圆
在圆 直径
直径 的延长线上,
的延长线上,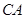 切圆
切圆 于
于 点,
点, 的平分线
的平分线 交
交 于点
于点 ,交
,交 于
于 点.
点.
(1)求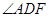 的度数;
的度数;
(2)若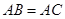 ,求
,求 .
.
已知f(x)为定义在[-1,1]上的奇函数,当x∈[-1,0]时,函数解析式f(x)=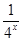 -
- (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
已知二次函数y=f(x)满足f(-2)=f(4)=-16,且f(x)最大值为2.
(1)求函数y=f(x)的解析式.
(2)求函数y=f(x)在[t,t+1](t>0)上的最大值.
某军工企业生产一种精密电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=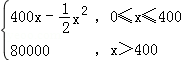 其中x是仪器的月产量.
其中x是仪器的月产量.
(1)将利润表示为月产量的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润.)
已知函数f(x)= ,且f(1)=3
,且f(1)=3
(1)求a的值;
(2)当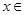
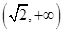 时,求函数f(x)的值域
时,求函数f(x)的值域
已知全集U={x|﹣5≤x≤3},A={x|﹣5≤x<﹣1},B={x|﹣1≤x<1},
(1)求∁UA,A∩(∁UB);
(2)若C={x|1﹣a≤x≤2a+1},且C⊆A,求实数a的取值范围.