(本小题满分13分)
若有穷数列 ,
,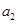 ,
,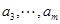 (
(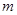 是正整数)满足条件:
是正整数)满足条件: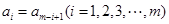 ,则称其为“对称数列”.例如,
,则称其为“对称数列”.例如,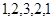 和
和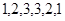 都是“对称数列”.
都是“对称数列”.
(Ⅰ)若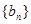 是25项的“对称数列”,且
是25项的“对称数列”,且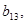

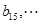 ,
,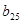 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求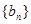 的所有项和
的所有项和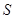 ;
;
(Ⅱ)若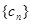 是50项的“对称数列”,且
是50项的“对称数列”,且

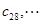 ,
, 是首项为1,公差为2的等差数列.求
是首项为1,公差为2的等差数列.求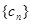 的前
的前 项和
项和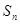 ,
,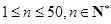 .
.
(本小题满分12分)已知函数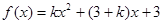 ,其中
,其中 为常数,且
为常数,且
(1)若 ,求函数
,求函数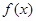 的表达式;
的表达式;
(2)在(1)的条件下,设函数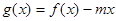 ,若
,若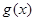 在区间
在区间 上是单调函数,求实数
上是单调函数,求实数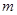 的取值范围;
的取值范围;
(3)是否存在实数 使得函数
使得函数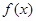 在
在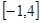 上的最大值是4?若存在,求出
上的最大值是4?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(满分12分)已知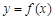 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当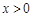 时,
时, .
.
(Ⅰ)求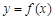 的解析式;
的解析式;
(Ⅱ)问是否存在这样的正数a, b使得当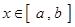 时,函数
时,函数 的值域为
的值域为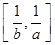 ,若存在,求出所有a, b的值,若不存在,说明理由.
,若存在,求出所有a, b的值,若不存在,说明理由.
(本小题满分12分)已知函数 f(x)=4x2-4ax+(a2-2a+2).
(1)若a=1, 求f(x)在闭区间[0,2]上的值域;
(2)若f(x)在闭区间[0,2]上有最小值3,求实数a的值.
(本小题满分12分 )已知定义在区间(﹣1,1)上的函数 是奇函数,且
是奇函数,且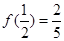 ,
,
(1)确定 的解析式;
的解析式;
(2)判断 的单调性并用定义证明;
的单调性并用定义证明;
(本题10分)设全集为R,集合A={x|3≤x<6},B={x|2<x<9}.
(1)分别求A∩B,(∁RB)∪A;[
(2)已知C={x|a<x<a+1},若C⊆B,求实数a的取值范围构成的集合