汽车是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对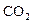 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 型品牌车各抽取
型品牌车各抽取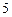 辆进行
辆进行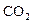 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: ).
).
| 甲 |
80 |
110 |
120 |
140 |
150 |
| 乙 |
100 |
120 |
 |
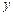 |
160 |
经测算发现,乙品牌车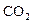 排放量的平均值为
排放量的平均值为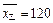
 .
.
(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合 排放量的概率是多少?
排放量的概率是多少?
(Ⅱ)若 ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车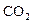 排放量的稳定性.
排放量的稳定性.
已知 的图象经过点
的图象经过点 ,且在
,且在 处的切线方程是
处的切线方程是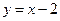
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(1)已知椭圆的焦点为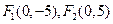 ,点
,点 在椭圆上,求它的方程(2)已知双曲线顶点间的距离为6,渐近线方程为
在椭圆上,求它的方程(2)已知双曲线顶点间的距离为6,渐近线方程为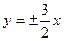 ,求它的方程.
,求它的方程.
求下列函数的导函数:
(1)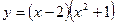
(2)
选作题,请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分,每道题满分10分)
22、选修4—1:几何证明选讲
如图,△ABC的角平分线AD的延长线交于的外按圆于点E。
(I)证明:△ABC∽△ADC
(II)若△ABC的面积为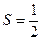 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。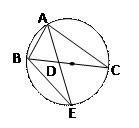
23、选修4—4:坐标系与参数方程
已知半圆C的参数方程
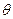 为参数且(0≤
为参数且(0≤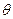 ≤
≤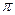 )
)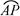 P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与的长度均为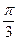 。
。
(I)求以O为极点, 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。
(II)求直线AM的参数方程。
24、选修4—5,不等式选讲
已知函数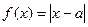

(I)若不等式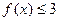 的解集为
的解集为 求a值。
求a值。
(II)在(I) 条件下,若 对一切实数
对一切实数 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
(本小题满分12分)如下图,某小区准备绿化一块直径为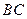 的半圆形空地,
的半圆形空地,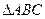 的内接正方形
的内接正方形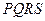 为一水池,
为一水池,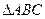 外的地方种草,其余地方种花.若
外的地方种草,其余地方种花.若
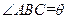 ,设
,设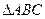 的面积为
的面积为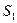 ,正方形
,正方形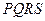 的面积为
的面积为 ,将比值
,将比值 称为“规划合理度”.
称为“规划合理度”.
(1)试用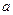 ,
, 表示
表示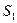 和
和 ;
;
(2)若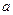 为定值,当
为定值,当 为何值时,“规划合理度”
为何值时,“规划合理度”
最小?并求出这个最小值.