已知 的图象经过点
的图象经过点 ,且在
,且在 处的切线方程是
处的切线方程是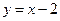
(1)求 的解析式;
的解析式;
(2)求 的单调递增区间
的单调递增区间
(本小题满分12分)已知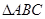 中,
中,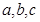 分别为内角
分别为内角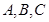 所对的边,且满足
所对的边,且满足 .
.
(Ⅰ)求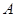 ;
;
(Ⅱ)现给出三个条件:①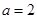 ②
②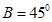 ③
③ .从中选出两个可以确定
.从中选出两个可以确定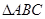 的条件,写出你的选择,并以此为依据,求出
的条件,写出你的选择,并以此为依据,求出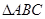 的面积.(只需写出一个选定方案并完成即可)
的面积.(只需写出一个选定方案并完成即可)
.(本小题满分12分)已知等差数列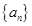 满足:
满足: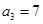 ,
,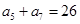 ,
,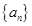 的前n项和为
的前n项和为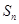 .
.
(Ⅰ)求通项公式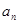 及前n项和
及前n项和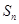 ;
;
(Ⅱ)令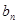 =
=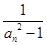 (n
(n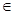 N*),求数列
N*),求数列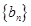 的前n项和
的前n项和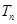 .
.
(本题满分14分)已知椭圆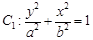
 的右顶点
的右顶点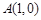 ,过
,过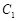 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为 .
.
(I) 求椭圆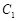 的方程;
的方程;
(II) 设点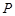 在抛物线
在抛物线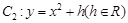 上,
上,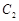 在点
在点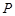 处的切线与
处的切线与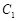 交于点
交于点 .当线段
.当线段 的中点与
的中点与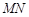 的中点的横坐标相等时,求
的中点的横坐标相等时,求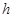 的最小值.
的最小值.
(本题满分15分)设函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)已知 对任意
对任意 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)试讨论方程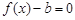 的零点个数.
的零点个数.
(本题满分15分) 如图,已知正方形 和矩形
和矩形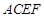 所在的平面互相垂直,
所在的平面互相垂直,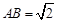 ,
,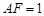 ,
, 是线段
是线段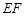 的中点.
的中点.
(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)试在线段 上确定一点
上确定一点 ,使得
,使得 与
与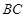 所成的角是
所成的角是 .
.