选作题,请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分,每道题满分10分)
22、选修4—1:几何证明选讲
如图,△ABC的角平分线AD的延长线交于的外按圆于点E。
(I)证明:△ABC∽△ADC
(II)若△ABC的面积为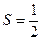 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。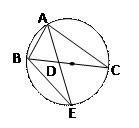
23、选修4—4:坐标系与参数方程
已知半圆C的参数方程
 为参数且(0≤
为参数且(0≤ ≤
≤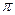 )
)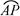 P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为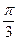 。
。
(I)求以O为极点, 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。
(II)求直线AM的参数方程。
24、选修4—5,不等式选讲
已知函数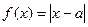

(I)若不等式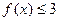 的解集为
的解集为 求a值。
求a值。
(II)在(I) 条件下,若 对一切实数
对一切实数 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
已知以角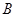 为钝角的的三角形
为钝角的的三角形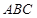 内角
内角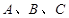 的对边分别为
的对边分别为 、
、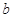 、
、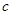 ,
,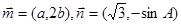 ,且
,且 与
与 垂直.
垂直.
(1)求角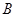 的大小;
的大小;
(2)求 的取值范围
的取值范围
在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=1.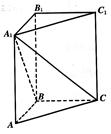
(1)求异面直线B1C1与AC所成角的大小;
(2)若该直三棱柱ABC-A1B1C1的体积为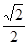 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.
已知函数
(1)求函数 的值域,并写出函数
的值域,并写出函数 的单调递增区间;
的单调递增区间;
(2)若 ,且
,且 ,计算
,计算 的值.
的值.
已知点 ,点
,点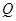 在曲线
在曲线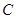 :
: 上.
上.
(1)若点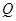 在第一象限内,且
在第一象限内,且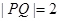 ,求点
,求点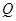 的坐标;
的坐标;
(2)求 的最小值.
的最小值.
定义在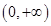 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有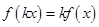 (
(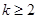 ,
, )成立,则称
)成立,则称 为
为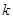 阶缩放函数.
阶缩放函数.
(1)已知函数 为二阶缩放函数,且当
为二阶缩放函数,且当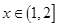 时,
时, ,求
,求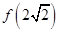 的值;
的值;
(2)已知函数 为二阶缩放函数,且当
为二阶缩放函数,且当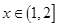 时,
时,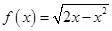 ,求证:函数
,求证:函数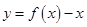 在
在 上无零点;
上无零点;
(3)已知函数 为
为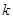 阶缩放函数,且当
阶缩放函数,且当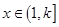 时,
时, 的取值范围是
的取值范围是 ,求
,求 在
在 (
(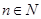 )上的取值范围.
)上的取值范围.