定义在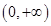 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有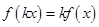 (
(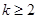 ,
, )成立,则称
)成立,则称 为
为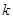 阶缩放函数.
阶缩放函数.
(1)已知函数 为二阶缩放函数,且当
为二阶缩放函数,且当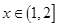 时,
时, ,求
,求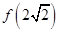 的值;
的值;
(2)已知函数 为二阶缩放函数,且当
为二阶缩放函数,且当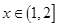 时,
时,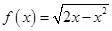 ,求证:函数
,求证:函数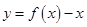 在
在 上无零点;
上无零点;
(3)已知函数 为
为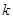 阶缩放函数,且当
阶缩放函数,且当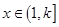 时,
时, 的取值范围是
的取值范围是 ,求
,求 在
在 (
(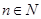 )上的取值范围.
)上的取值范围.
(12分) 函数 对任意
对任意 都有
都有 .
.
(1)求 和
和 的值;
的值;
(2)数列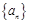 满足:
满足: ,数列{an}是等差数列吗?请给予证明;
,数列{an}是等差数列吗?请给予证明;
在第(2)问的条件下,若数列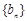 满足
满足 ,
, ,试求数列
,试求数列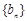 的通项公式.
的通项公式.
(12分) 设数列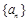 的前n项和为
的前n项和为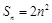 ,
,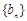 为等比数列,且
为等比数列,且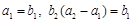 .
.
(1)求数列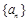 和
和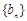 的通项公式;
的通项公式;
(2)设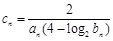 ,求数列
,求数列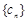 的前n项和
的前n项和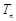 .
.
(12分) 在△ABC中,a、b、c分别为角A、B、C的对边,且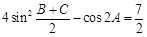 ,
,
(1)求 的度数;
的度数;
(2)若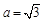 ,
,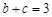 ,求b和c的值.
,求b和c的值.
(13分) 已知等比数列{an}中,a2=2,a5=128.
(1) 求通项an;
(2) 若bn = log2an,数列{bn}的前n项和为Sn,且Sn = 360,求n的值.
(13分) 已知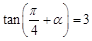 ,且
,且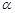 为锐角.
为锐角.
(1) 求 的值;
的值;
(2) 求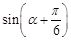 的值.
的值.