某 单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛
单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛 ,其中
,其中 男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给
男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给 以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中提取10人,然后再从这10人中 选4人,那么至少有1人是“运动健将”的概率是多少?
选4人,那么至少有1人是“运动健将”的概率是多少?
(2)若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并
的分布列,并 求
求 的数学期望.
的数学期望.
已知函数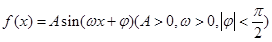 ,的部分图象如图所示.
,的部分图象如图所示.
(1) 求函数 的解析式;
的解析式;
(2) 如何由函数
 的图象通过适当的平移与伸缩变换得到函数
的图象通过适当的平移与伸缩变换得到函数 的图象,写出变换过程.
的图象,写出变换过程.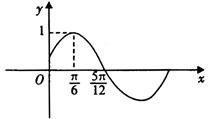
已知奇函数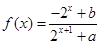 是定义域为
是定义域为 的减函数
的减函数
(Ⅰ)求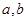 的值;
的值;
(Ⅱ)若对任意的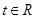 ,不等式
,不等式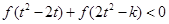 恒成立,求
恒成立,求 的取值范围;
的取值范围;
已知三角形 的顶点坐标为
的顶点坐标为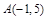 ,
,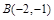 ,
,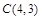 ,
,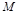 是
是 边上的中点。
边上的中点。
(Ⅰ)求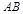 边所在直线的方程;
边所在直线的方程;
(Ⅱ)求中线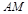 的长;
的长;
(Ⅲ)求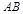 边的高所在直线的方程。
边的高所在直线的方程。
如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1.