如图,在直三棱柱ABC﹣A1B1C1(侧棱和底面垂直的棱柱)中,平面A1BC⊥侧面A1ABB1,AB=BC=AA1=3,线段AC、A1B上分别有一点E、F且满足2AE=EC,2BF=FA1.
(1)求证:AB⊥BC;
(2)求点E到直线A1B的距离;
(3)求二面角F﹣BE﹣C的平面角的余弦值.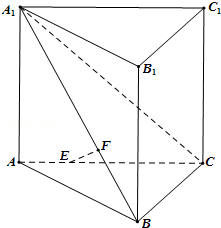
已知椭圆C的中心在原点,焦点在x轴上,离心率为 ,短轴长为4
,短轴长为4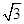 .
.
(I)求椭圆C的标准方程;
(II)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点,且直线AB的斜率为 .
.
①求四边形APBQ面积的最大值;
②设直线PA的斜率为 ,直线PB的斜率为
,直线PB的斜率为 ,判断
,判断 +
+ 的值是否为常数,并说明理由.
的值是否为常数,并说明理由.
已知数列{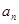 }的前n项和
}的前n项和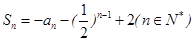 ,数列{
,数列{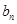 }满足
}满足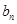 =
=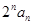 .
.
(I)求证数列{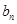 }是等差数列,并求数列{
}是等差数列,并求数列{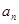 }的通项公式;
}的通项公式;
(Ⅱ)设 ,数列{
,数列{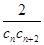 }的前n项和为Tn,求满足
}的前n项和为Tn,求满足 的n的最大值.
的n的最大值.
如图1, 的直径AB=4,点C、D为
的直径AB=4,点C、D为 上两点,且
上两点,且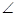 CAB=45°,
CAB=45°,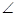 DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
DAB=60°,F为弧BC的中点.沿直径AB折起,使两个半圆所在平面互相垂直,如图2.
(I)求证:OF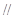 平面ACD;
平面ACD;
(Ⅱ)求二面角C—AD—B的余弦值;
(Ⅲ)在弧BD上是否存在点G,使得FG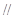 平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.
平面ACD?若存在,试指出点G的位置;若不存在,请说明理由.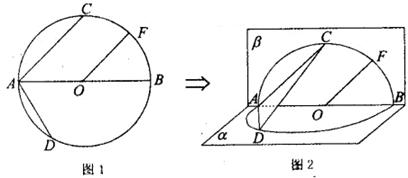
中国航母“辽宁舰”是中国第一艘航母,“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性,科学家对蒸汽轮机进行了170余项技术改进,增加了某项新技术,该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测.假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 、
、 、
、 .指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
.指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
(I)求该项技术量化得分不低于8分的概率;
(II)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望.
在△ABC中,已知A= ,
, .
.
(I)求cosC的值;
(Ⅱ)若BC=2 ,D为AB的中点,求CD的长.
,D为AB的中点,求CD的长.