已知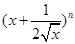 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;
的值;
(2)求展开式中系数最大的项.
(本小题满分12分)
已知函数 .
.
(Ⅰ) 求函数 的单调递增区间;
的单调递增区间;
(Ⅱ) 已知 中,角
中,角 所对的边长分别为
所对的边长分别为 ,若
,若 ,
, ,求
,求 的面积
的面积 .
.
(满分8分)
已知 是实数,函数
是实数,函数 。
。
(I)若 ,求
,求 的值;
的值;
(II)在(1)的条件下,求曲线 在点
在点 处的切线方程;
处的切线方程;
(III)求 在区间
在区间 上的最大值。
上的最大值。
(满分6分)
已知函数 ,且
,且 。
。
(I)求 ;
;
(II)判断 的奇偶性;
的奇偶性;
(III)函数 在
在 上是增函数还是减函数?并证明你的结论。
上是增函数还是减函数?并证明你的结论。
(满分6分)
(I)已知 ,且
,且 为第三象限角,求
为第三象限角,求 的值;
的值;
(II)求函数 的最大值。
的最大值。
(本小题满分14分)已知圆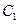 :
: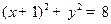 ,点
,点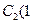 ,
,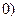 ,点
,点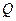 在圆
在圆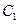 上运动,
上运动,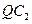 的垂直平分线交
的垂直平分线交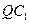 于点
于点 .
.
(Ⅰ)求动点 的轨迹
的轨迹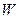 的方程;
的方程;
(Ⅱ)设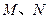 分别是曲线
分别是曲线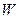 上的两个不同点,且点
上的两个不同点,且点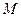 在第一象限,点
在第一象限,点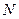 在第三象限,若
在第三象限,若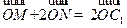 ,
,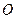 为坐标原点,求直线
为坐标原点,求直线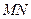 的斜率
的斜率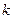 ;
;
(Ⅲ)过点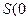 ,
,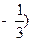 且斜率为
且斜率为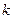 的动直线
的动直线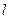 交曲线
交曲线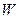 于
于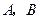 两点,在
两点,在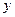 轴上是否存在定点
轴上是否存在定点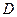 ,使以
,使以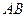 为直径的圆恒过这个点?若存在,求出
为直径的圆恒过这个点?若存在,求出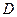 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.