从参加环保知识竞赛的学生中抽出60名,将其成绩整理后画出的频率分布直方图如下.观察图形,回答下列问题: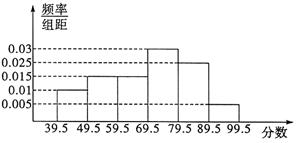
(1)49.5——69.5这一组的频率和频数分别为多少?
(2)估计这次环保知识竞赛成绩的中位数及平均成绩.(精确到小数点后一位)
已知:四边形ABCD是空间四边形,E, H分别是边AB,AD的中点,F, G分别 是边CB,CD上的点,且
是边CB,CD上的点,且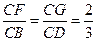 .
.
求证:(1)四边形EFGH是梯形;
(2)FE和GH的交点在直线AC上.
求经过三点A ,B(
,B(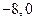 ),C(0,6)的圆的方程,并指出这个圆半径和圆心坐标.
),C(0,6)的圆的方程,并指出这个圆半径和圆心坐标.
(本小题满分13分)
已知函数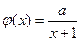 ,
,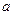 为正常数.
为正常数.
(1)若 ,且
,且 ,求函数
,求函数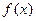 的单调增区间;
的单调增区间;
(2)若 ,且对任意
,且对任意 ,
,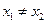 ,都有
,都有 ,求
,求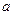 的的取值范围.
的的取值范围.
(本小题满分13分)
给定椭圆 >
> >0
>0 ,称圆心在原点
,称圆心在原点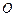 ,半径为
,半径为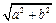 的圆是椭圆
的圆是椭圆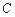 的“准圆”
的“准圆” 。若椭圆
。若椭圆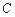 的一个焦点为
的一个焦点为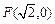 ,其短轴上的一个端点到
,其短轴上的一个端点到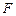 的距离为
的距离为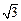 。
。
(1)求椭圆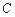 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点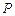 是椭圆
是椭圆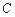 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点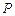 作直线
作直线 ,使得
,使得 与椭圆
与椭圆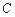 都只有一个交点。求证:
都只有一个交点。求证: ⊥
⊥ .
.
(本小题满分13分)
某电视生产企业有A、B两种型号的电视机参加家电下乡活动,若企业投放A、B两种型号电视机的价值分别为a、b万元,则农民购买电视机获得的补贴分别为 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)求当投放B型电视机的金额为多少万元时,农民得到的总补贴最大?