如图，已知椭圆C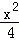：y21的上、下顶点分别为A、B，点P在椭圆-优题课

题文

如图，已知椭圆C：+y²=1的上、下顶点分别为A、B，点P在椭圆上，且异于点A、B，直线AP、BP与直线l：y=﹣2分别交于点M、N，
（1）设直线AP、BP的斜率分别为k₁、k₂，求证：k₁•k₂为定值；
（2）当点P运动时，以MN为直径的圆是否经过定点？请证明你的结论．

科目数学题型解答题难度较易

登录免费查看答案和解析

相关试题

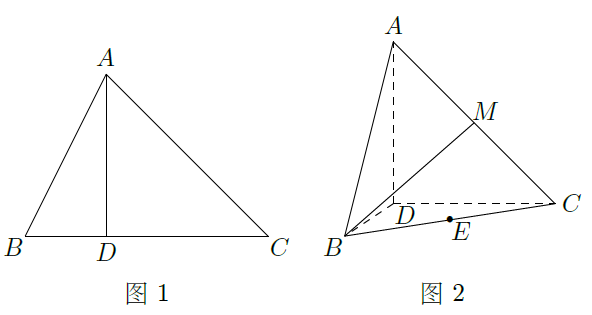
如图1， $∠ A C B = 45^{°}, B C = 3$ ，过动点 $A$ 作 $A D ⊥ B C$ ，垂足 $D$ 在线段 $B C$ 上且异于点 $B$ ，连接 $A B$ ，沿 $A D$ 将 $△ A B D$ 折起，使 $∠ B D C = 90^{°}$ （如图2所示）．
（Ⅰ）当 $B D$ 的长为多少时，三棱锥 $A - B C D$ 的体积最大；
（Ⅱ）当三棱锥 $A - B C D$ 的体积最大时，设点 $E, M$ 分别为棱 $B C, A C$ 的中点，试在棱 $C D$ 上确定一点 $N$ ，使得 $E N ⊥ B M$ ，并求 $E N$ 与平面 $B M N$ 所成角的大小．

已知等差数列 $\{a_{n}\}$ 前三项的和为 $- 3$ ，前三项的积为 $8$ .
（Ⅰ）求等差数列 $\{a_{n}\}$ 的通项公式；
（Ⅱ）若 $a_{2}$ ， $a_{3}$ ， $a_{1}$ 成等比数列，求数列 $\{|a_{n}|\}$ 的前 $n$ 项和

已知向量 $a = (\sin ω x - \sin ω x, \sin ω x)$ ， $b = (- \cos ω x - \sin ω x, 2 \sqrt{3} \cos ω x)$ ，设函数 $f (x) = a \cdot b + λ$ $x \in R$ 的图象关于直线 $x = π$ 对称，其中 $ω$ ， $λ$ 为常数，且 $ω \in (\frac{1}{2}, 1)$ .
（Ⅰ）求函数 $f (x)$ 的最小正周期；
（Ⅱ）若 $y = f (x)$ 的图象经过点 $(\frac{π}{4}, 0)$ ，求函数 $f (x)$ 在区间 $[0, \frac{3 π}{5}]$ 上的取值范围.

(本题满分14分)抽样调查30个工人的家庭人均月收入，得到如下数据：(单位：元)
404　444　556　430　380　420　500　430　420　384　420　404　424　340　424　412　388　472　358　476　376　396　428　444　366　436　364　438　330　426
(1)取组距为60，起点为320，列出样本的频率分布表；
(2)画出频率分布直方图；
(3)根据频率分布直方图估计人均月收入在[440,500)中的家庭所占的百分比．

(本题满分12分)有朋自远方来，他乘火车、轮船、汽车、飞机来的概率分别为0.3,0.2,0.1,0.4.
试问：(1)他乘火车或乘飞机来的概率；
(2)他不乘轮船来的概率；
(3)如果他来的概率为0.5，请问他有可能是乘何种交通工具来的．
即他不乘轮船来的概率为0.8.

试卷网试题网古诗词网作文网范文网