一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1) 标签的选取是无放回的; (2) 标签的选取是有放回的.
某校高三年级学生600名,从参加期中考试的学生中随机抽出某班学生(该班共50名同学),并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下表:
| 分组 |
频数 |
频率 |
 |
2 |
0.04 |
 |
4 |
0.08 |
 |
8 |
0.16 |
 |
11 |
0.22 |
 |
15 |
0.30 |
 |
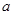 |
 |
 |
4 |
0.08 |
| 合计 |
50 |
1 |
(1)写出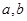 的值;
的值;
(2)估计该校高三学生数学成绩在120分以上学生人数;
(3)该班为提高整体数学成绩,决定成立“二帮一”小组,即从成绩在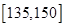 中选两位同学,来帮助成绩在
中选两位同学,来帮助成绩在 中的某一位同学,已知甲同学的成绩为56分,乙同学的成绩为145分,求甲乙在同一小组的概率.
中的某一位同学,已知甲同学的成绩为56分,乙同学的成绩为145分,求甲乙在同一小组的概率.
在数列 中,
中,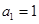 ,数列
,数列 是首项为9,公比为3的等比数列.
是首项为9,公比为3的等比数列.
(Ⅰ)求 的值;
的值;
(Ⅱ)求数列 的前n项和
的前n项和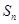 .
.
已知函数 ,其中
,其中 .
.
(Ⅰ)当 时,求不等式
时,求不等式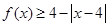 的解集;
的解集;
(Ⅱ)已知关于x的不等式 的解集为
的解集为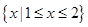 ,求
,求 的值 .
的值 .
在直角坐标系 中,以
中,以 为极点,
为极点, 轴正半轴为极轴建立极坐标系.圆
轴正半轴为极轴建立极坐标系.圆 ,直线
,直线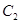 的极坐标方程分别为
的极坐标方程分别为 .
.
(Ⅰ)求 与
与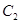 交点的极坐标;
交点的极坐标;
(Ⅱ)设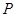 为
为 的圆心,
的圆心, 为
为 与
与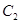 交点连线的中点.已知直线
交点连线的中点.已知直线 的参数方程为
的参数方程为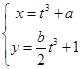 (
(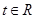 为参数),求
为参数),求 的值.
的值.
如图,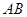 是圆
是圆 的直径,直线
的直径,直线 与圆
与圆 相切于
相切于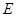 ,
,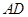 垂直
垂直 于
于 ,
, 垂直
垂直 于
于 ,
, 垂直
垂直 于
于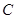 ,
, 垂直
垂直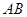 于
于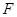 ,连接
,连接 ,证明:
,证明:
(Ⅰ) ;
;
(Ⅱ)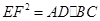 .
.