已知数列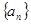 中,当
中,当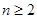 时,总有
时,总有 成立,且
成立,且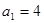 .
.
(Ⅰ)证明:数列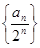 是等差数列,并求数列
是等差数列,并求数列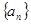 的通项公式;
的通项公式;
(Ⅱ)求数列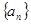 的前
的前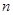 项和
项和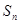 .
.
已知正方体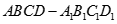 ,
, 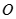 是底
是底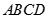 对角线的交点.
对角线的交点.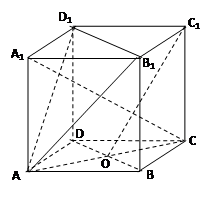
求证:(Ⅰ)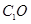 ∥面
∥面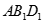 ;
;
(Ⅱ)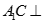 面
面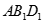
已知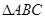 的三个内角
的三个内角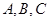 所对的边分别为a,b,c,向量
所对的边分别为a,b,c,向量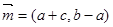 ,
, ,且
,且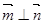 .
.
(Ⅰ)求角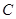 的大小;
的大小;
(Ⅱ)若向量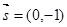 ,
,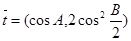 ,试求
,试求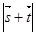 的取值范围
的取值范围
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: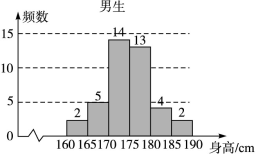
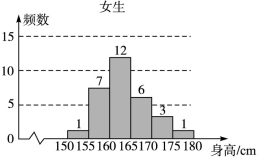
(Ⅰ)估计该校男生的人数;
(Ⅱ)估计该校学生身高在170~185 cm之间的概率;
(Ⅲ)从样本中身高在180~190 cm之间的男生中任选2人,求至少有1人身高在185~190 cm之间的概率.
设数列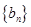 满足
满足 ,若数列
,若数列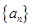 满足:
满足: ,且当
,且当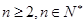 时,
时,
(I) 求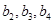 及
及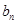 ;
;
(II)证明: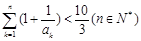 ,(注:
,(注: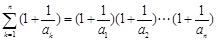 ).
).