(本小题14分)抛物线 与直线
与直线 相交于
相交于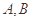 两点,且
两点,且
(1)求 的值。
的值。
(2)在抛物线 上是否存在点
上是否存在点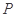 ,使得
,使得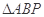 的重心恰为抛物线
的重心恰为抛物线 的焦点
的焦点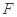 ,若存在,求点
,若存在,求点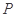 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
已知各项均为正数的数列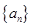 的前
的前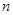 项和为
项和为 ,且对任意正整数
,且对任意正整数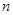 ,点
,点 都在直线
都在直线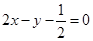 上.
上.
(1)求数列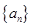 的通项公式;
的通项公式;
(2)若 设
设 求数列
求数列 前
前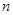 项和
项和 .
.
已知数列 是等差数列,且
是等差数列,且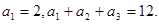
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令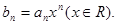 求数列
求数列 前n项和的公式.
前n项和的公式.
已知函数f(x)= (a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(a、b为常数),且方程f(x)-x+12=0有两个实根为x1=3,x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式f(x)<  .
.
某村计划建造一个室内面积为800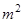 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1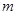 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 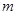 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
已知不等式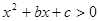 的解集为
的解集为
(1)求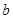 和
和 的值; (2)求不等式
的值; (2)求不等式 的解集.
的解集.