要对一块长60米、宽40米的矩形荒地 进行绿化和硬化.
进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形 面积的
面积的 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为 和
和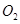 ,且
,且 到
到 的距离与
的距离与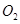 到
到 的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
伦敦奥运会将于2012年7月27日开幕,组委会备选的开幕式甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)将下表填完整:
| 身高(厘米) |
176 |
177 |
178 |
179 |
180 |
| 甲队(人数) |
3 |
4 |
0 |
||
| 乙队(人数) |
2 |
1 |
1 |
(2)甲队队员身高的平均数为厘米,乙队队员身高的平均数为厘米;
(3)你认为哪支仪仗队更为整齐?简要说明理由.
平行四边形ABCD中,AB=5,AD=8,∠C、∠D的平分线分别交 AD、BC与点E、F,且AF⊥BC.
(1)求tan∠ADF;
(2)求CE的长.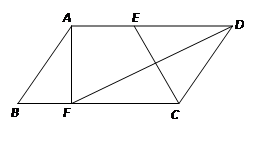
解方程: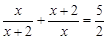
计算: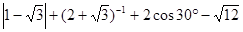
已知:半圆 的半径
的半径 ,
, 是
是 延长线上一点,过线段
延长线上一点,过线段 的中点
的中点 作垂线交
作垂线交 于点
于点 ,射线
,射线 交
交 于点
于点 ,联结
,联结 .
.
(1)若 ,求弦
,求弦 的长.
的长.
(2)若点 在
在 上时,设
上时,设 ,
, ,求
,求 与
与 的函数关系式及自变量
的函数关系式及自变量 的取值范围;
的取值范围;
(3)设 的中点为
的中点为 ,射线
,射线 与射线
与射线 交于点
交于点 ,当
,当 时,请直接写出
时,请直接写出 的值.
的值.